Question
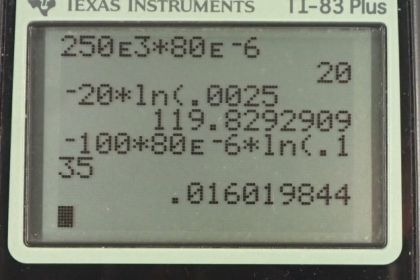
Figure 21.55 shows how a bleeder resistor is used to discharge a capacitor after an electronic device is shut off, allowing a person to work on the electronics with less risk of shock. (a) What is the time constant? (b) How long will it take to reduce the voltage on the capacitor to 0.250% (5% of 5%) of its full value once discharge begins? (c) If the capacitor is charged to a voltage through a resistance, calculate the time it takes to rise to (This is about two time constants.)
Final Answer
Solution video
OpenStax College Physics, Chapter 21, Problem 71 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
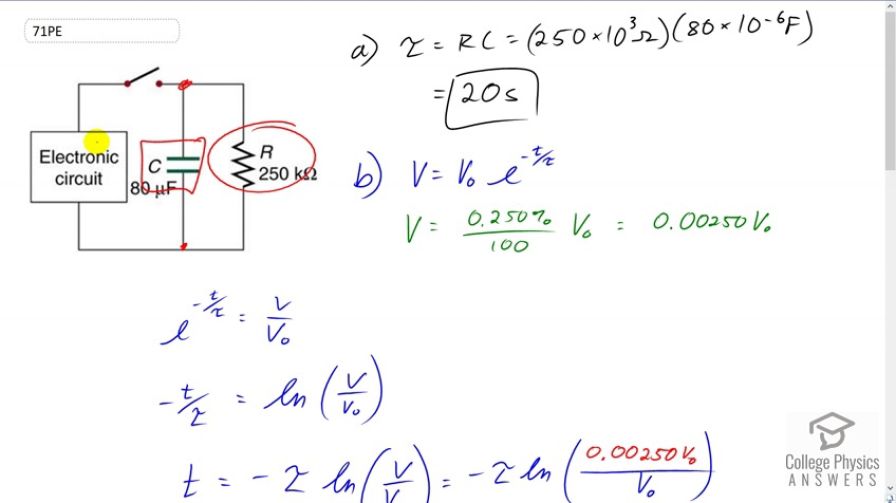
This is College Physics Answers with Shaun Dychko. This bleeder resistor is used to discharge this capacitor after the circuit is done being used and somebody wants to work on it and they don't want to be touching a charged capacitor. And so by attaching this resistor here and here, that causes a current to flow through the resistor and some energy gets dissipated. And while the charge moves through the circuit and goes through the other plate in the capacitor until there is an equal amount charge in both plates, in which case, there's no voltage across it anymore. So, we're going to find the time constant. It's resistance times capacitance. That's 250 times ten to three ohms times 80 times ten to the minus six Farads, giving us 20 seconds for the time constant. And part b asks us to find how long will it take to reduce the voltage on the capacitor to one quarter percent of its full value. So, this is the formula for the voltage of a discharging capacitor. And so the voltage will be the initial voltage times e to the power of negative time divided by the time constant. And so we're told that the voltage should be 0.25 percent, which is 0.25 divided by a hundred times the initial voltage V naught. And so that is 0.0025 V naught. And if we rearrange this and divide both sides by V naught, we're going to solve for t, by the way. You got this line here and then we take the natural logarithm of both sides. And on the left side, we end up with negative t over tau. And on the right side we have natural logarithm of V over V naught. So time is negative tau times natural logarithm of V over V naught. And then substituting finally for V in place of, we put 0.0025 V naught in place of V. We can see that the V naught is cancel and we have there the time is going to be negative over the time constant multiplied by natural logarithm of 0.0025. So it's negative 20 seconds times natural log of 0.0025, which is 120 seconds. So, it's about two minutes. And then in part c, were asked, if the capacitor is charged to a voltage of V naught with a 100 Ohm resistance. Find the time it takes to rise to 0.865 V naught. So, how will it take before it's 86 and a half percent charged. This is the formula for a voltage across a charging capacitor. It's the final or maximum voltage times one minus e to the negative t over the time constant RC. And the voltage is 0.865 times V naught. And so we substitute that in for V. And then divide both sides by V naught. And so we have one minus e to the negative t over RC equals 0.865. And then, move this to the right hand side and move this to the left hand side. So, one minus 0.865 is 0.135. And this e term became positive. And so e to the negative t over RC is 0.135. Then take the natural logarithm of both sides and we have negative t over RC equals natural log of 0.135. And then multiply both sides by negative RC. And we got time as negative RC times natural log of 0.135. So it's negative 100 Ohms times 80 times ten to the minus six Farads times natural log of 0.135 which is 16 milliseconds.