Question
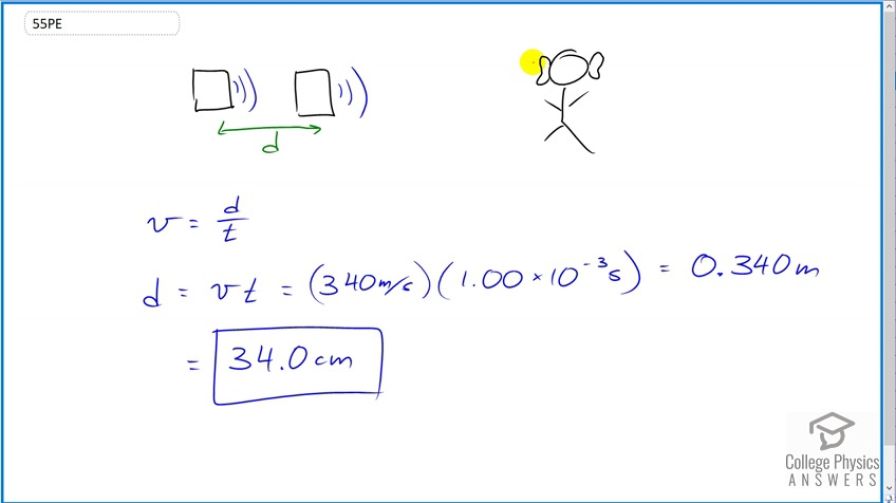
Your ear is capable of differentiating sounds that arrive at the ear just 1.00 ms apart. What is the minimum distance between two speakers that produce sounds that arrive at noticeably different times on a day when the speed of sound is 340 m/s?
Final Answer
Solution video
OpenStax College Physics, Chapter 16, Problem 55 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Human ears have a time resolution of one millisecond, meaning that it's possible for people to distinguish sounds occurring at different times when the time separation between the two sounds is as short as one millisecond. The geometry of the situation where we're looking for the minimum separation between speakers such that we have a one millisecond difference in the sounds coming from them would be like this where you have the speakers in a line along a straight line towards the person. The person was standing in front of the speakers here, they would be equidistant from the speakers and there'd be no difference in the time it takes for the sounds to reach the person. The person is here, and strictly speaking, I suppose the person should be standing facing the speakers so that their ears, both ears, are equidistant from the two speakers because this ear here is going to hear the sounds at a slightly different time than this ear. But that's a very minor point because this is a very small distance here. Okay. So the speed of the wave, or anything really, is the distance that it travels divided by time and we're given the wave speed of 340 meters per second and we're also given the time of one millisecond. So we'll solve for d by multiplying both sides by t, and then switch the sides around. So d is the wave speed multiplied by the time. That's 340 meters per second times one millisecond written as one times ten to the minus three seconds which gives 34.0 centimeters and that is this distance d such that the sound from this far speaker reaches the person's ears one millisecond after the same sound came from this speaker that's closer.
