Question
Suppose you attach the object with mass to a vertical
spring originally at rest, and let it bounce up and down. You release the object from rest at the spring’s original rest length. (a) Show that the spring exerts an upward force of on the object at its lowest point. (b) If the spring has a force constant of and a 0.25-kg-mass object is set in
motion as described, find the amplitude of the oscillations. (c) Find the maximum velocity.
Final Answer
- See solution video for derivation
Solution video
OpenStax College Physics, Chapter 16, Problem 17 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
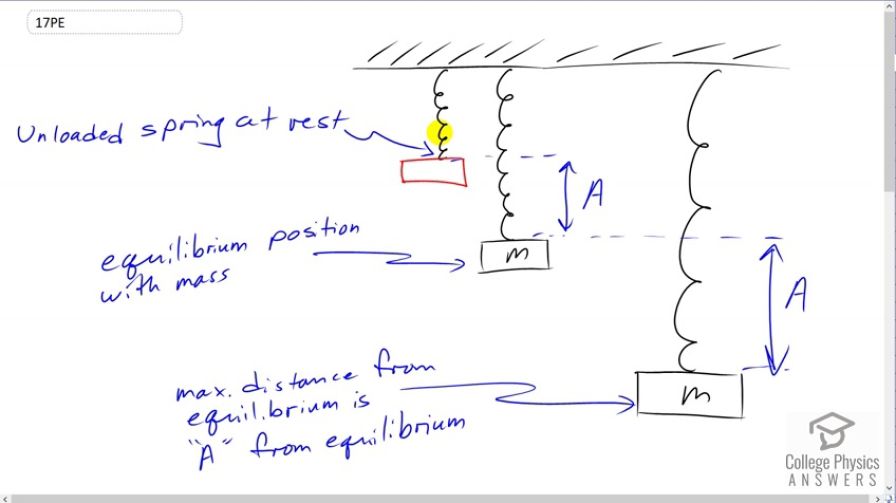
This is College Physics Answers with Shaun Dychko. So a mass is added to a spring. And this is done at the spring's original rest position, its unloaded rest position. So, the spring is just hanging in there by itself and then some mass is hung on it. And if it were to bounce up and down, up and down, up down to the point where it finally stopped, it would stop in this position, this is called the equilibrium position with some mass added. And this distance between the spring's rest position when it's unloaded, and this position when it's in at rest with a mass loaded on it. This is the amplitude of the motion, because the amplitude is defined as the distance between the equilibrium position and the maxima of its positions. So this would be a maxima and that it's the minimum stretch of this spring, that's where it started. And then, when the mass is initially hung on the spring, it's going to go pass the equilibrium position for this extreme of stretching. And again, it will go a distance A which is the amplitude from the equilibrium to this maximum stretching. So, we know at equilibrium that the force upwards which is the force to the spring, k times the amount by which the spring is stretched which is A, the amplitude, that has to equal the force of gravity downwards. And so we can say that, for this position. And then from that we could figure out the amplitude in terms of m, g and k by dividing both sides by k. And then at the maximum extension here, maximum position downwards, we know that the force is going to be k times two times the amplitude because the spring has been stretched by one amplitude to get to this position. And then by another amplitude again to get to this position for a total of two times A from the initial rest position of the unloaded spring. And then, so we can substitute this mg over k in place of A and we get k times two times mg over k and the k is cancel, giving us two mg. And this is what we wanted to show is that the force upwards due to the spring is two times mg at this lowest position. Then the question in part b is, figure out what the amplitude will be given the certain mass and spring constant? So, the mass is 0.25 kilograms times 9.81 newtons per kilograms divided by ten newtons per meter, giving an amplitude of 0.245 meters. And then maximum speed, we have a formula that says is the amplitude times the square root of the spring constant divided by mass, so it's 0.24525 meters times square root ten over 0.25 kilograms giving 1.55 meters per second.