Question
A wave traveling on a Slinky® that is stretched to 4 m takes 2.4 s to travel the length of the Slinky and back again. (a) What is the speed of the wave? (b) Using the same Slinky stretched to the same length, a standing wave is created which consists of three antinodes and four nodes. At what frequency must the Slinky be oscillating?
Final Answer
Solution video
OpenStax College Physics, Chapter 16, Problem 61 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
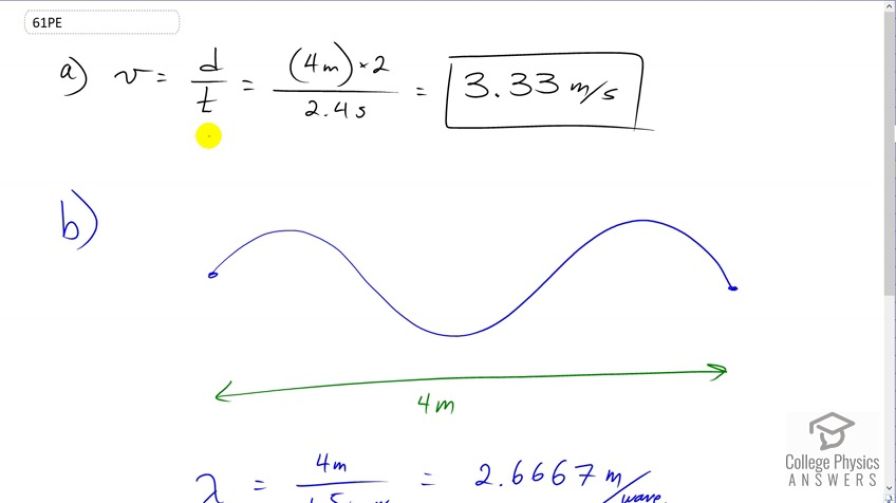
This is College Physics Answers with Shaun Dychko. A wave travels on the Slinky, traveling the full length of the Slinky twice in 2.4 seconds. So it goes to the end of the Slinky and then comes back. The Slinky length is four meters and so it goes to the end four meters and then comes back four meters for a total of eight meters in 2.4 seconds. So the speed of the wave is eight divided by 2.4 which is 3.33 meters per second. The next question is what is the frequency of the wave? Well we'll figure out the frequency using this formula for the speed of the wave which is frequency times wavelength, by figuring out what the wave length is and dividing both sides by lambda to solve for f being v over lambda. I drew a picture here to figure out what lambda is. Now the full length of the Slinky is four meters and we're told that there are three anti-nodes -- did I say that right, three anti-nodes? Yeah, and four nodes. The nodes are the positions that do not move on a standing wave. The anti-nodes are the positions of maximum displacement from equilibrium. Okay, so the crests in other words or the anti-nodes. So, three anti-nodes and four nodes and this is a full four meters. We can see that one wave length goes to here starting at this node, and then beyond that is a half wave length and so in four meters we have one and a half wave lengths. The lambda then is four divided by one and a half which is 2.6667 meters per wave. We plug that in down here for lambda and so the frequency is speed, 3.3333 meters per second that we figured out in part A, and then divide by the wave length that we just found using that picture. This gives a frequency of one and a quarter Hertz.

