Question
To increase intensity of a wave by a factor of 50, by what factor should the amplitude be increased?
Final Answer
Solution video
OpenStax College Physics, Chapter 16, Problem 65 (Problems & Exercises)
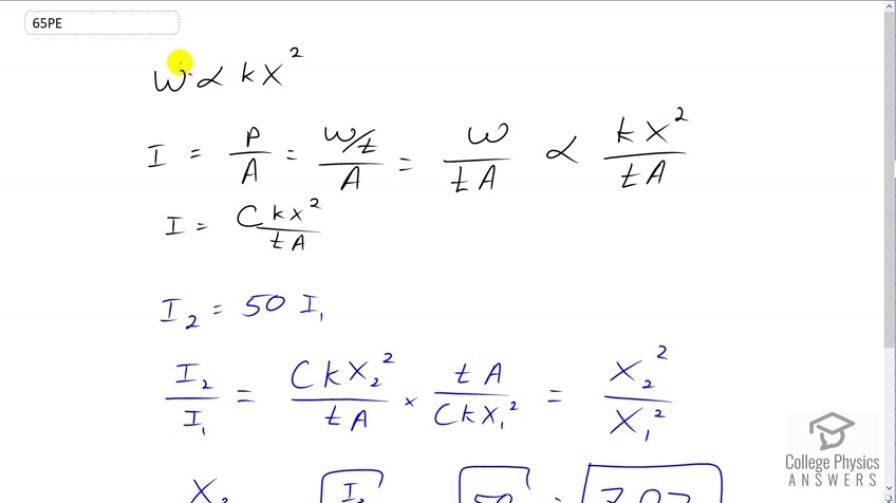
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. So to increase the intensity of a wave by a factor of 50, our factor with the amplitude needs to be increased. We know that the work done by the wave or its energy in other words, is proportional to some, you know, spring constant so to speak, times its amplitude squared. Being proportional means that it's going to be some additional constant here that we don't know. So, intensity is power per area and power is the rate at which work is done, so work divided y time. This can be written as w over t A. This is proportional to k X squared over t A since work is proportional to this. Then we'll put some constant in here just because this proportional symbol is sometimes a bit confusing to work with. It just means that there's some constant of proportionality that we don't know and we can just write it down as the letter c. Intensity two is meant to be 50 times intensity one and so we'll take intensity two divided by intensity one, and here's intensity two, c k amplitude two squared, divided by time times area. Then divided by intensity one which is the same as multiplying by its reciprocal. So multiply by t A over c k X one squared. Almost everything cancels except for the X two squared over X one squared. So when we take the square root of both sides here, we get that the ratio of amplitudes is the square root of the ratio of the intensities. I two is 50 times I one and so this I two divided by I one is 50. So we have square root of 50 is 7.07. So a wave that is 7.07 times greater amplitude will have an intensity that is 50 times.
