Question
Suppose the length of a clock’s pendulum is changed by 1.000%, exactly at noon one day. What time will it read 24.00 hours later, assuming it the pendulum has kept perfect time before the change? Note that there are two answers, and perform the calculation to four-digit precision.
Final Answer
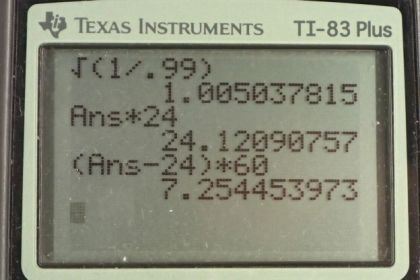
When the length is shortened by 1.000%, the indicated time will be 12:07:15
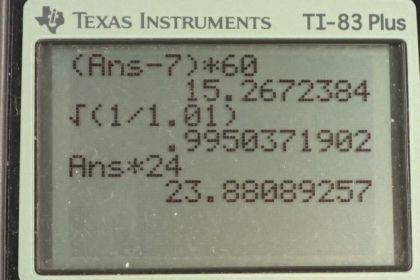
When the length is extended by 1.000%, the indicated time will be 11:52:51
Solution video
OpenStax College Physics, Chapter 16, Problem 33 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The way in which a pendulum clock keeps time is by counting the number of swings of the pendulum and then it's calibrated such that it will indicate a certain amount of time passing depending on a certain number of swings of the pendulum. So we're going to figure out what are the number of swings of the pendulum when you have it calibrated properly, in which case you have the correct frequency to indicate a passage of 24 hours of time. So N p is proper, p for proper, the number of swings that it has without changing the length of its pendulum. So it's the frequency which is the number of swings per second multiplied by the number of seconds that gives the number of swings. Frequency is the reciprocal of period so we can also write this as the amount of time that has passed divided by the time per swing. So that's t times one over two pi times square root g over L. This is the reciprocal of the period formula for a pendulum. So consider the first case, case A, where the length A is one percent less than the length L. L with no subscript indicates the length when the pendulum is working properly, where it's calibrated properly such that, you know, this many swings indicates 24 hours of time has passed and in fact it's true that 24 hours of time has actually passed. Okay. So, in this case here, the number of swings that will occur is going to be the amount of time that's passed, times one over two pi times square root g over this new length L a. But L a is going to be 0.99 times L because it's one percent less and so it is 99 percent of L. This t here is the real time that has in fact passed. So now this could be 24 hours for example but the number of swings that will occur is going to be different from the number of swings that are supposed to occur. So the clock will not say the 24 hours have passed despite the fact that 24 hours in fact has passed. Okay. So we're going to find the ratio of the number of swings that occur in case A, divided by the proper number of swings that one would expect in 24 hours. It's going to be t times one over two pi times square root g over 0.99 L. This is our expression here for N a. Then dividing by N p means multiplying by its reciprocal. So we have one over t times two pi times square root L over g. So I've taken the reciprocal of this and written it here. Now most things cancel here except for the square root one over 0.99 and then multiply both sides by N p. We get that the number of swings that are going to occur is going to be N p times square root one over 0.99 which is 1.00503782 times N p. So how much time will the clock have indicated passing? Well, it's going to swing this many times, this number 1.00503782 times N p, that's what we figured out here. Multiply that by 24 hours of time actually passing for every N p swings because N p again represents the number of swings that should occur in 24 hours. We'll find that the clock is going to indicate that 24.1209076 hours have passed. This is going to be a discrepancy then of this minus 24 hours of time actually passing and then we'll convert that into minutes by multiplying by 60 minutes per hour. We get 7.254454 minutes is the discrepancy of this clock with a shorter pendulum. Then to get the seconds part of this discrepancy we subtract 7 minutes away and then multiply what's left by 60 seconds per minute and we get 15.27 seconds. So this clock when the time is shortened is going to indicate a time of 12:07:15. So it's going to indicate a time seven minutes and fifteen seconds after noon. Okay. So this clock is running fast with a shortened pendulum. So then we do the same thing again when the pendulum in case B is longer than what it's supposed to be. So we're going to say that the length is one percent longer than L. So the number of times that the pendulum in case B, capital N b, is going to be t times one over two pi times g over L b. But L b is now 1.01 times L, 1.01 representing one percent more than L. So N b over N p is t times one over two pi times g over 1.01 L, times two pi square root Lover g. That's the reciprocal of this again, with a one over t by the way. Okay. Then this works out to square root one over 1.01 and so we can figure out the number of swings in this case here. It's going to be square root one over 1.01 times the proper number of swings. That's 0.9950372 times the proper number of swings. So the amount of time that this clock will indicate passing is going to be this number of swings multiplied by 24 hours per N p swings. So that's 0.9950372 N p which is the number of swings in this case B times 24 hours for every N p. We get 23.88089 hours is the amount of time that will be indicated passing on this pendulum with a longer pendulum. So the discrepancy is going to be this amount of time minus 24 hours converted into minutes. So that's negative 7.1466 minutes and then we'll subtract away seven from this number of minutes to get the seconds portion. The time when this pendulum is lengthened on this clock is going to be 12 minutes minus this discrepancy of seven minutes and 9 seconds. So this works out to 11:52:51 will be the time on the clock when the pendulum has been lengthened.