Solution video
OpenStax College Physics, Chapter 16, Problem 6 (Problems & Exercises)
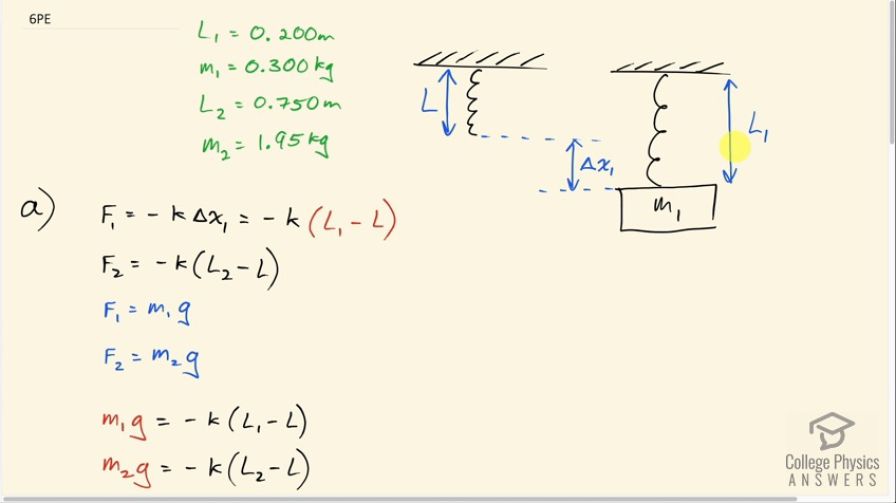
Calculator Screenshots
Comments
I was able to get the same answer for part a by using the equation F=-kx, with F being the difference in weight force between the two hanging masses and x being the difference in length of the spring between the two hanging masses. Is this also a valid way to solve the problem, or does it just happen to work out that way for this problem?
Hi ts, thanks for the question. You've derived a good method, and look at 3:02 in the video -- it's saying algebraically what you have said with words! Your method finds how the length changes with load forces on the spring, which is the purpose of the spring constant.
Best wishes with your studies,
Shaun
For part B, if we take the length of the spring as a negative value (you mention that the -0.2m is negative because it is a downward displacement), why do we not also take mg, the weight force of the hanging object to be negative as well, since it points in the downward direction?
More specifically, wouldn't only the magnitudes of kx and mg be equal, rather than the direction, thus we wouldn't want to use a negative sign in front of kx for part B? I was able to get the same answer without using any negative signs at all.
Hi ts,
You're making a good point. It turns out that this solution essentially has a double negative error - which makes it turn out right! The force of gravity should be negative, as you say, since it's down. Furthermore, the spring force is not equal to gravity, but rather - the spring force is equal to the negative of gravity since they're in opposite directions. That double negative would make the solution the same as shown in the video. In the video I put gravity as positive, and also said the spring force is equal to gravity. In any case, I hope it's clear enough, but I can see a case for redoing the video in order to clear up this negative sign issue.
Thanks again,
Shaun
I'm confused, why are we using a mass if the problem asks the length with NO mass hanging from it?
Hello jsotosky, you mean for part (b), right? Hooke's Law says the spring force is the spring constant times the amount of stretch of the spring. If we can find out how much the spring stretches with a mass hanging on it, and we know the final length, then we can find the unloaded length. We know the spring force since that will be equal to the weight of the hanging mass - which is why we need the mass for this part of the solution. The question gives us the final length with either mass (using either mass would be fine for part (b)), and I replaced the amount by which the spring stretches with the expression where is the loaded length of 0.200m and is the unloaded length we're trying to find. The rest is algebra to solve for .
Hope this helps,
Shaun



