Question
Suppose you have a total charge that you can split in any manner. Once split, the separation distance is fixed. How do you split the charge to achieve the greatest force?
Final Answer
Solution video
OpenStax College Physics, Chapter 18, Problem 19 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
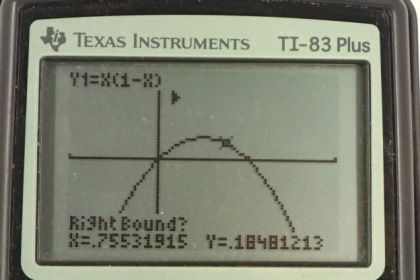
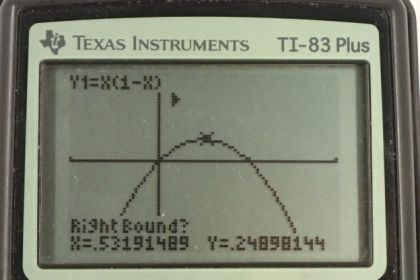
This is College Physics Answers with Shaun Dychko. We have some amount of charge called Q total and we're going to split it into two portions such that we have the maximum force between these two portions. So the first portion is going to be some factor a times the total, and the next portion will be some factor b times the total. When you take a times the total plus b times the total you're meant to have the total in the end which means that when you divide both sides by q total, you'll see that a plus b is one. That means b is one minus a when you subtract a from both sides. Okay. So we can substitute that in here so that we have only one variable that we're going to maximize. It's this expression a times one minus a that we want to maximize. Now this is a quadratic equation and that means it's a parabola and the parabola is going to have a maximum. We know that because the coefficient of the squared term is negative which means the parabola is upside down. We're going to figure out what is the x coordinate of this vertex. So there's a couple of ways to do that. One is the graphical method using the graphing calculator and I'll show a bunch of screen shots below this video on how to do that. The algebraic method is called Completing the Square. So I like to make the coefficient of the squared term positive so I'm going to multiply both sides by negative one first of all. So we have negative y is a squared minus a. Then to complete the square we take half the coefficient of the linear term which is to say half the coefficient of the term which is to the power of one. That coefficient is not written but it's presumed to be the number one. So half of that is one half and then you square that. That's going to be one quarter and then you add that to both sides. So we're going to add one quarter to both sides of this expression. So we have negative y plus a quarter equals a squared minus a plus a quarter. Now this is because of the way we've figured out what this term should be, this is a perfect square. We can factor it into a binomial and so it's going to be factored as a minus a half, squared. Then we can bring this over to the right hand side and then multiply both sides by negative one and we get our equation here which is in a form that we can interpret. When you have a variable plus or minus some number and then in bracket squared plus some other number, each of these corresponds to a thing on the graph. So we can plot this without making a table of values because that takes too long. We're going to instead just plot it based on understanding how this form of the equation turns into a graph. So the vertex is going to be at a positive one half because that is when this term is zero and that's when y will be its maximum of a quarter. So we have a y coordinate of a quarter when a is one half. So that answers our question about where you'll have a maximum, for what value of a we have a maximum. The answer is one half. So -- yeah, just to expand on that a bit, any other value for a would result in a negative number here which we'd take away from this one quarter. So everything else is going to be less than a quarter. So it'll be a parabola that's upside down and something like this. If you want to be more precise you can figure out where these x intercepts are -- our a axis intercepts I guess I should say, and so on. Anyway, for our purposes we're done because we know what value of a maximizes this thing here. So by maximizing a times one minus a, we're maximizing this force. So the total charge should be split in half because a should be half and also b, which is one minus a, is also going to be half.