Question
Suppose a speck of dust in an electrostatic precipitator has protons in it and has a net charge of –5.00 nC (a very large charge for a small speck). How many electrons does it have?
Final Answer
Solution video
OpenStax College Physics, Chapter 18, Problem 5 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
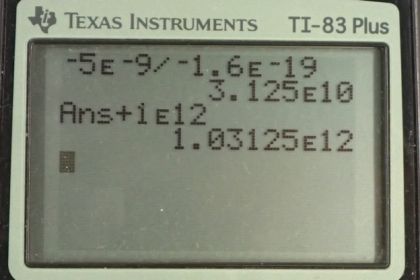
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The speck of dust in this electrostatic precipitator which is probably in a smoke stack to remove dust particles and it has one times ten to the 12 protons. And there is a net charge on it of negative five nanocoulombs, and nano is the prefix meaning times ten to the minus nine. And because this is a net charge, this is the number of electrons that are in excess of the number of protons. So we’ll figure out this number of excess electrons and then add that to the number of protons since each of these protons are balanced by a corresponding electron and in addition to those that balance all these protons, there are this many excess ones. So we add the excess to the number that balance each of these protons to get the total number of electrons. So we take the charge of negative five times ten to the minus nine coulombs times one electron for every negative 1.6 times ten to the minus 19 coulombs and we get 3.125 times ten to the ten electrons, in excess of the number of protons. Now add these excess electrons to all the electrons that are balancing each of these protons and we have one times ten to the 12 electrons plus 3.125 times ten to the ten electrons, giving 1.0313 times ten to the 12 electrons. And this number will be precise to this place value here because this number is precise to that place value and this place value here corresponds to the two in this number and this number actually should have only three significant figures in the final rounded number but I keep extra numbers here because this is an intermediate calculation and so this number is going to get rounded to five significant figures in the end. When you add these two together, you get 1.03125 times ten to the 12 but since this number here is precise only to the place value with digit two and likewise this one’s precise only to this place value here, they both have the same limits of precision which is this place value there, so we round the two into a three, so 1.0313 times ten to the 12 is our answer.