Question
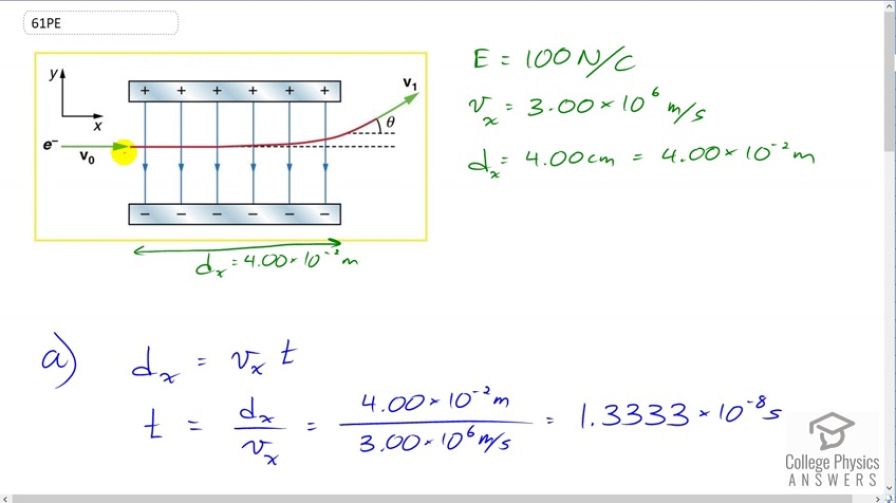
Figure 18.57 shows an electron passing between two charged metal plates that create an 100 N/C vertical electric field perpendicular to the electron's original horizontal velocity. (These can be used to change the electron's direction, such as in an oscilloscope.) The initial speed of the electron is , and the horizontal distance it travels in the uniform field is 4.00 cm. (a) What is its vertical deflection? (b) What is the vertical component of its final velocity? (c) At what angle does it exit? Neglect any edge effects.
Final Answer
Solution video
OpenStax College Physics, Chapter 18, Problem 61 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
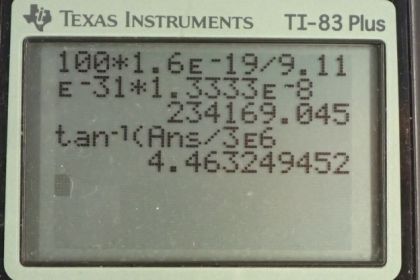
This is College Physics Answers with Shaun Dychko. We have an electron with some initial speed of three times ten to the six meters per second and that initial speed is entirely in the x direction. And it’s going to pass through this electric field that is between these charge plates, and it will exit the plates going at some velocity v1 and it’ll have a vertical component to its velocity as well as a horizontal component. So in part a, we figure out what is this vertical displacement and in part b, we figure out what is the vertical component of its velocity after it passes through the plates and then part c is what is this angle. So part a, first of all we need to figure out how long does it spend between the plates and we use that to eventually calculate the vertical displacement because it’s going to be one half times the vertical acceleration times time squared. So let’s first figure out the time. We know that the horizontal component of its velocity will be constant because this electric field will impart a vertical velocity and it’ll have no effect on its horizontal velocity that it had initially so the horizontal component of velocity stays constant. And so we know the x displacement which we’re given is four centimeters, is going to equal the horizontal component of velocity multiply by time, and so we’ll solve for t by dividing both sides by vx here. And so t is dx divided by vx, and the horizontal displacement is four centimeters written as times ten to the minus two meters, and divided by the x component of its velocity which is three times ten to the six meters per second. And we get 1.3333 times ten to the minus eight seconds, keeping lots of digits in there since this is an intermediate calculation. Now the vertical component of its displacement will be the initial y component of its velocity times time, plus one half times vertical acceleration times time squared, but there is no initial component to its velocity vertically, and so this term is zero. So this works out to one half ay t squared. Now the y component of the net force equals mass times the y component of acceleration and this has to equal the force exerted by the electric field on the charge. And so we’ll solve for the vertical acceleration by dividing both sides by m here, and so vertical acceleration is the electric field strength times the charge divided by its mass, and then we substitute that into the vertical acceleration, we do that here. So the vertical component of its displacement after passing through the plate is one half Eq over m times time squared. So it’s one half times 100 newtons per coulomb, electric field strength, times 1.6 times ten to the minus 19 coulombs, elementary charge, divided by the mass of an electron 9.11 times ten to the minus 31 kilograms, times the time squared, and we get 1.56 millimeters. Then in part b, we want to know what is the vertical component of its velocity after it passes between the plates. Well that’s going to equal the initial component of its velocity that is vertical which is zero, plus the vertical acceleration times time. And the acceleration we already found is Eq over m from up here, so we can substitute that again down here so we’re taking that multiplying it by time. And so electric field strength times elementary charge divided by mass of electron multiply by time, giving us 2.34 times ten to the five meters per second will be the vertical component of its velocity. And the angle of its velocity will be the inverse tangent of the y component divided by the x component, so that’s inverse tangent of this answer for part b, divided by the x component that we’re given, and this is 4.46 degrees above the positive horizontal.