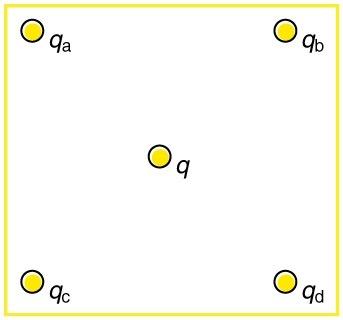
Question
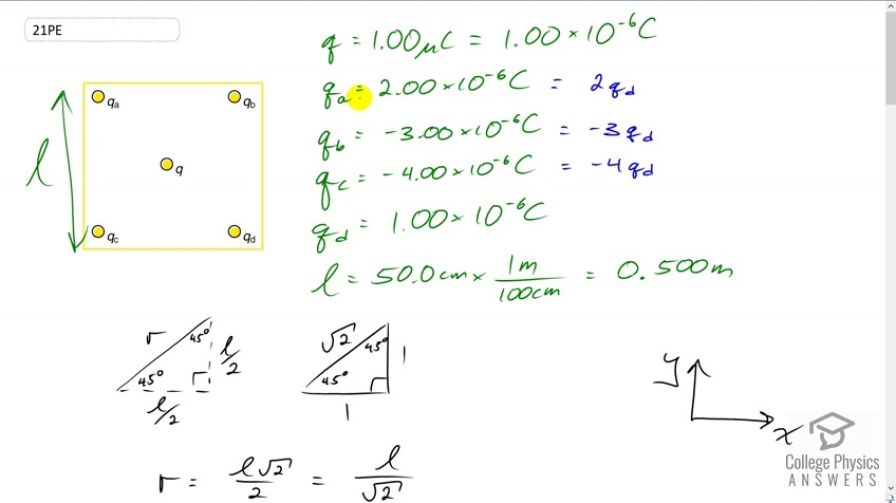
Find the total Coulomb force on the charge in Figure 18.53, given that , , , , and .The square is 50.0 cm on a side.
Final Answer
Solution video
OpenStax College Physics, Chapter 18, Problem 48 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the total Coulomb force on this charge. It's in the middle of the square. And since there are four charges in each of the corners and we're told that each of those charge is r. And we're told the length of a side on the square is 50 centimeters and then convert that into meters. And we're told that the charge in the middle is one micro Coulomb. I've written each of this charges as multiples of this smallest charge. Just because that's going to make her work a little bit easier, I won't have to put in numbers in the Algebra. I'll be able to just use letters and in our arithmetic will actually just amount to this simple arithmetic because we've expressed things in terms of qd. So, instead of plugging in, four due to charge c, instead of plugging in negative four micro Coulombs into the Coulombs equation here, I'm just going to write four multiplied by qd instead. And that saves the amount of calculation we have to do. Anyway, you'll see that in a second. So, to start with, we need to figure out what is the distance between the charge and the center and the charge at the corner. And they all have the same distance because this is a square, so each of these diagonals are the same. They're all length r. And this length r makes the hypotenuse of a triangle which is a right triangle, which is an isosceles right triangle and an isosceles right triangle is a special triangle where the sides are related by these factors, so that the two legs could be of length one and then the hypotenuse would be root two multiplied by whatever the legs length are. So, the leg lengths are l over two. So this is half of the square side length. And this also is half of the square side length there and so we've drawn that here. And so we multiplied each leg by l over two. And so this hypotenuse then is l over two multiplied by root two. And this works out to l over root two. Now, if you don't like that method, that's fine. The alternative would be to say that, well, since we know that these angles here are 45 degrees. And the sign of 45 degrees is the opposite l over two, divided by the hypotenuse which is r. And then we could solve this for r by saying it's l over two divided by sine 45. And then plug that into a calculator after you substitute 0.5 meters for l and you'll figure out what r is. But we could also say that, sine 45 is one over root two which we can tell from the special triangle because one is the opposite and root two is the hypotenuse and sine is 45 is the opposite divided by the hypotenuse. And this works out to l root two over two which simplifies the l over root two. And that's what we have over here. So, we're going to consider the x direction first and we're going to find the components of each of the four forces. Each of the forces due to the four different charges that are in the x direction. And then we'll add them together. And then we'll get the resultant x component. So the force due to charge a, on the force in the center is k times whatever the charge a is, times the charge in the center q divided the distance between them squared. And charge qa is two times charge qd because we're told qa is two micro Coulombs and qd is one micro Coulombs, that means that qa is two times qd. And so I substitute two times qd in place of qa. And then we're going to find its x component and since this force is directed along the diagonal of the square the x component is going to be--- well, let's draw the force here. Here's the force due to charge a and this is a repulsive force because the charge in the center and the charge at this corner here ar oth positive, and so they're repelling. And so force a will be down into the right. And this is going to be at an angle of 45 degrees. And its x component will be Fa times cos 45. We have cos 45 as the adjacent over the hypotenuse. And the adjacent is what we want to find, Fax and that's divided by the hypotenuse. And we can solve for Fax by saying it's Fa times cos 45. And cos 45 is one over root two. So we have Fa times one over root two. And this is what you're going to see here. So we have force a, which we have figured out here times over root two. Now the same analysis applies to all the other forces because they're all acting along the square diagonals. And so they're all going to be multiplied by cos 45. And the only difference is their sign and the factor by which they are a multiple of qd. And so, we'll look at force due to charge b, and because b is negative, it's going to be attracting the charge in the center. And so it's x component would be to the right. And so it is also positive. And so the negative or the positive that I'm going to write in down here is nothing to do with the sign of the charge. Like I'm not going to write a negative in this force term here because this force term, the sign of it is meant to indicate as direction. And so by looking at this picture and seeing that it's the negative charge, we know the direction will be to the right in the x direction. And so we're going to put a positive there. And this positive takes in account, the signs of the charges and just indicates its direction. So that's positive k times three qdq over r squared times one over root two. So, we're taking the cos 45 multiplied by this to find its x component. And then for force c, charge c is negative. And so it's going to be exerting a force down into the left. And so its x component will be to the negative. And so we have a negative k times four qd because that's the magnitude of charge c, is four times charge qd times q over r squared times one over root two. And then d is a positive charge and so it's going to be up into the left cause it's going to repel the force or the charge in the center. And so it's x component will be negative, as well. So we have a negative there times qd times q over r squared times one over root two. And then we combine all these to find the resultant x component. And so we have Fax plus Fbx plus Fcx plus Fdx. And all of these forces have a lot of common factors, kqdq over r squared times one over root two. And so I factored all those out, leaving behind only these factors in front of qd. So we have a positive two, positive three and negative four and then negative one. So two three minus four minus one. And all these works out to zero. So there's no x component left at all on the charge in the center. And then we have the y direction. And the process is the same, and even this component factor is the same because the sine of 45 is the same as the cosine of 45, they're both the same. And so it's one of our root two again. And charge a is down into the right, so y component will be negative. We just put a minus sign in front of that here. And then b is attracting the charge in the center, so it's y component will be positive. d is going to have a positive y component and charge c is going to have a negative y component. And so we have all those reflected here, positives and negatives as needed. And then, add them all together, factoring out the common factors. We have negative two, positive three, negative four and positive one. And this works out to negative two. So there is going to be a y component and because it's negative, it is directed downwards. And this r squared, well, r is l over root two, we've figured that out a while ago. And we'll make that substitution here. And so, negative two over root two times one over root two squared, that's a bit of a confusing thing in there. But this root two and the denominator becomes two after it’s squared. And so multiply top and bottom by two and this two will disappear and the top will become negative four. And negative four divided by root two is two root two, because we have four over root two here. Let's multiply top and bottom by two. Now this two cancels with this two that's going to end up being there after squaring. So we end up with the four on the top. And four can be thought of as two times root two times root two, still over root two. And then this root two is cancel leaving us with two root two. Okay, so that's where this comes from. So if negative two root two time kqdq over l squared and plug in numbers and then celebrate with our answer. So we have negative root two root two times the Coulombs Constant times one micro Coulomb for the charge qd and then one micro Coulomb for the charge on the center divided by the side legs of the square, 0.5 meters squared, giving us negative 0.102 Newtons. And that is 0.102 Newtons downwards. There we go. Congratulations if you follow that all the way through.
