Video Transcript
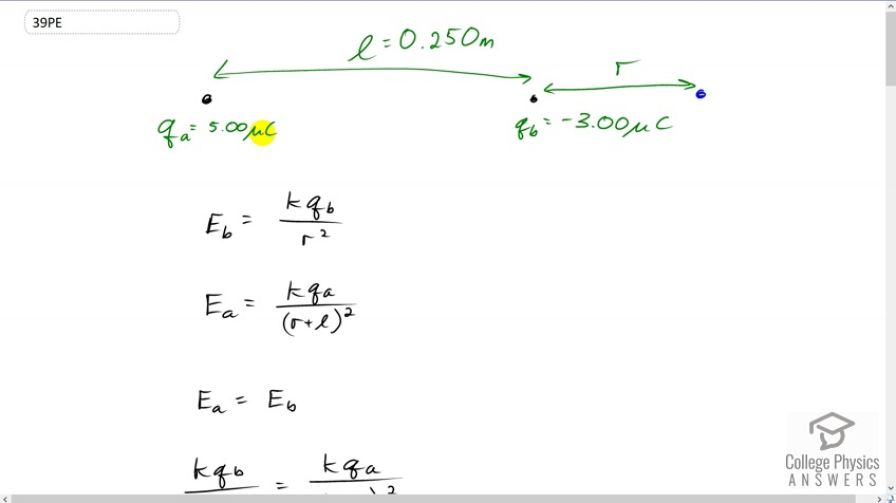
This is College Physics Answers with Shaun Dychko. We're told that there are two charges 0.25 meters apart. One charge I call q a is five micro-coulombs and the other charge q b is negative three micro-coulombs. The question says, figure out the location where we can put a third charge so that there'd be zero net force on it. So in other words, we're looking for a place where the electric field ends up being zero. So, there's an electric field due to charge b and a different electric field due to charge a. We need to find a place where they have equal magnitude in opposite directions. So, it helps to figure out what region this point will be in and we can figure out the region without any arithmetic just by using the concept of electric field. So, if you consider this region over here to the left of the positive charge, then this will never have a zero electric field because there is going to be a repulsion from this positive charge and there's going to be an attraction to this negative charge. But since the positive charge has greater magnitude than the negative charge, the repulsion that any third charge placed anywhere to the left of q a, will always -- there'll always be greater repulsion from this one than attraction to this one because this charge has a greater magnitude. We're closer to it than charge b. Then consider a positive test charge between these two charges then it would experience a repulsion from q a and at the same time an attraction to q b. So certainly the net force will be to the right. So there is no position between here where the electric field will be zero. But if you consider a position to the right of charge b there will be a place where the electric field is zero because at this point a positive test charge placed here will experience an attraction to charge b and a repulsion from charge a. You could say the same for a position to the left of charge a, though what makes to the right of charge b different is that since charge b is of smaller magnitude, it's okay to be closer to it and further away from charge a. But this greater distance from charge a is compensated for by the fact that charge a's magnitude is bigger at five micro-coulombs versus only three micro-coulombs for charge b. So there will be a sweet spot here such that the electric field is zero and we're closer to charge b and so it'll have a greater electric field due to charge b on account of being closer to it. But since charge b has a smaller magnitude charge, there will be a point where that electric field due to charge b is of equal magnitude to the electric field due to charge a and despite being further away from a, that is compensated for by the greater magnitude charge of charge a. Okay. So in algebraic terms we would say that the electric field due to charge b is Coulomb's constant times q b divided by this distance r squared. The electric field due to charge a will be Coulomb's constant times charge a, divided by this distance r which is from charge b plus this distance l separating the two charges, and that's squared. These electric fields have to be equal in order to have zero net field. So we can equate these two expressions and so we have k q bover r squared, equals k q a over r plus l squared. Then cancel the k's and then raise both sides to the exponent negative one in order to get our unknown in the numerator. So this is like taking the reciprocal of both sides, so we have r squared over q b equals r plus l all squared, over q a. Then multiply both sides by q b and then take the square root of both sides. This ends up giving us r equals square root of q b over q a times r plus l to the power of one. Then we distribute this square root factor into the brackets, multiply both terms inside by that and we have r equals r times square root q b over q a plus l times square root q b over q a. Then bring this term to the left side by subtracting it from both sides and then factor out the common factor r and you get r times one minus square root q b over q a equals l times square root q b over q a. Then divide both sides by this bracket and you solve for r. So that's l times square root q b over q a, divided by one minus square root q b over q a. So we have 0.25 meters is what l is, that's the separation between the charges, times the square root of three micro-coulombs divided by five micro-coulombs. Now notice I did not change the units into base units, normally I would turn this into three times ten to the minus six coulombs. You could do that if you wanted but it's okay to take a shortcut here because when you divide one number by another if the units are the same, those units will cancel. So it doesn't matter what the units are so long as they are the same, and these are both micro-coulombs. So that's fine. So let me divide by one minus square root three micro-coulombs over five micro-coulombs and you get 0.859 meters. So this position here is 0.859 meters from charge b on the opposite side to charge a. You have to say on the opposite side to charge a because if you say 0.859 meters and that's all you say, it's ambiguous because maybe you mean here, 0.859 meters. But we say 0.859 meters on the opposite side of charge a. Okay, so that's the answer there. Then this question goes on. There's a part B and it says suppose the charges q a and q b are of the same sign, they're both positive. Now, where would our position be such that there is zero electric field? If you consider this position here, there's going to be repulsion on a positive test charge there from both q a and q b, so clearly that's not a zero electric field. Likewise over here, there would be a repulsion from both and so the electric field would be pointing that way. But in between, there will be a place where there is zero electric field. It'll be somewhere to the right of center because it'll have to be closer to this smaller charge q b in order to have equal magnitude compared to the electric field due to charge a. So I've set it up such that our distance r is now with respect to charge a and the distance from this position of zero electric field to charge b we're going to express in terms of l and r. So, it's going to be this full separation between the charges l minus r, the distance from q a. So we have the electric field due to charge a equals the electric field due to charge b. So k q a over r squared equals k q b over l minus r squared. Then take the reciprocal of both sides after also canceling the common factor k, and you get r squared over q a equals l minus r squared over q b. Then multiply both sides by q a -- whoops, that's a q a there -- and that cancels that, and then take the square root of both sides. You get r is the square root of q a over q b times l minus r to the power of one. We'll distribute this into the brackets, and we have l times q a over q b, square rooted, minus r times square root q a over q b. Then add r square root q a over q b to both sides. We end up with r plus r times square root q a over q b equals l times square root q a over q b. Then factor the r out, and then you get this bracket, one plus square root q a over q b, and then divide both sides by that bracket. Then you end up with solving for r. It's l times square root q a over q b divided by one plus square root q a over q b. So that's 0.25 meters, times the square root of five micro-coulombs over three micro-coulombs, divided by one plus square root five micro-coulombs over three micro-coulombs. This means it'll be at a position of 0.141 meters away from the five micro-coulomb charge, and that is between the charges.