Question
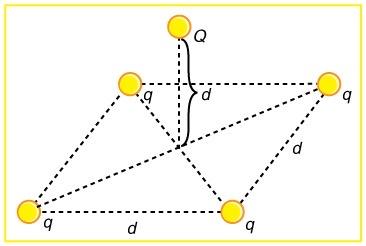
(a) In Figure 18.59, four equal charges lie on the corners of a square. A fifth charge is on a mass directly above the center of the square, at a height equal to the length of one side of the square. Determine the magnitude of in terms of , , and , if the Coulomb force is to equal the weight of . (b) Is this equilibrium stable or unstable? Discuss.
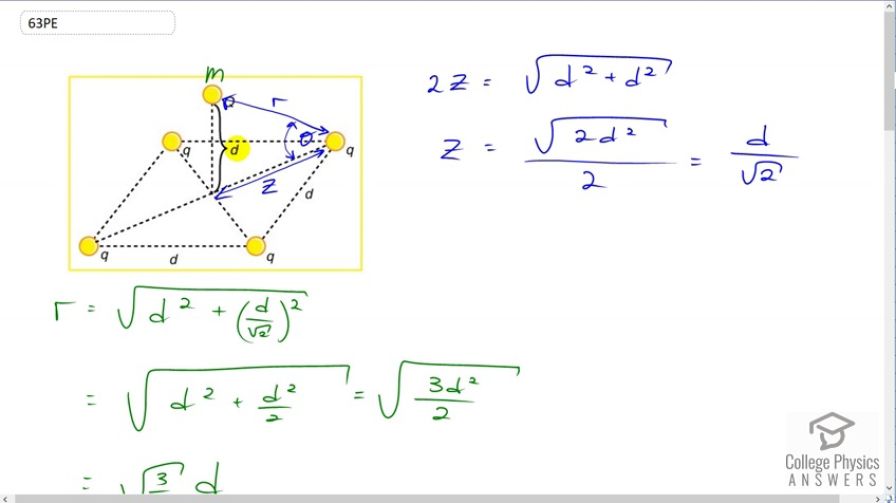
Final Answer
- This is a stable equilibrium since movements horizontally will result in a net horizontal component to restore the mass back to its original position.
Solution video
OpenStax College Physics, Chapter 18, Problem 63 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. In this picture, we have a mass m with a charge capital Q on it, which is some distance d above the center of a square. And on the corners of the square are four equal charges of magnitude little q, and the square have a side length of d as well. So what should little q be in order to create a repulsion force on this mass m upwards that will be equal to the mass’s force of gravity downwards. So we want the force of gravity down to be equal to the total upwards force exerted by each of these charges on the four corners. So this mass m is some distance little r from each of the corners, and we need to figure out what little r is in order to calculate the force of electrostatic repulsion between these corners and the charge capital Q. And to figure out r, we need to know what is this diagonal in here, we’ll call that z. And this z will be half of the diagonal of the square, and so I say two times little z is going to equal the square root of one side squared plus the other side squared, so I’m using the Pythagorean Theorem to figure out what is this diagonal. And then we need to take half of that diagonal to figure out what is z. So z is going to be square root of two times d squared, all over two, which works out to d over root two. And then after knowing z, we’ll figure out what little r is by saying little r is the hypotenuse of this triangle in yellow and that’s going to be the square root of the height d squared plus this little z which is d over root two squared. This is square root of d squared plus d squared over two, and that is square root of three d squared over two, which is simplified as square root three over two times d to the power of one. Now, we say that the gravity downwards on this mass which is mg is going to equal four times the y component of the electrostatic repulsion from one corner. So each of these charges are going to exert a force at some angle, and let’s consider this charge here and then this charge on the opposite corner will exert the same magnitude force at this angle and the x components of each will cancel, and the y components of each will add together. And this is what I’m referring to, is this is the y component and we want four of them because there are four corners, each exerting the same y component on this mass in the middle, and the x components are balanced out by the opposite corners. So we have four times the y component of one of the corner repulsion force. So what is that y component? Well that’s going to be the Coulomb force, Coulomb’s constant, times the corner charge little q, times the middle charge capital Q, over r squared, times sine of this angle theta where theta is between the diagonal of the square and this line connecting the corner to the mass. Now sine of this angle is going to be the opposite of this triangle divided by its hypotenuse, and so the opposite is little d, and the hypotenuse is little r, so I can write d over r in place of sin theta, and that’s what I did here. So Fy is going to be kqQ times d over r cube. So we substitute all this in to here for Fy. So I’ve written mg equals four times kqQd over r cube and r is root three over two d, that’s what we figure out up here, we figured that out there, and we substitute that in and then we get four times kqQ over d squared, because we have d to the power of one in the numerator and then d cube in the denominator, so that makes d squared in the denominator. And then to deal with this root three over two cube business in the denominator, and instead multiplying by root two over three, multiplying by its reciprocal, I don’t really like dividing a fraction by a fraction and so whenever I see that I always multiply by the denominator’s fraction’s reciprocal, so multiplying by root two over three to the power of three of course. And so root two over three to the power of three, you could plug that into your calculator and get a decimal and multiply by four, that would be fine, but I prefer to give an exact answer. So an exact answer would mean don’t use a calculator, and we can do that here because well, root two over three cube is the same as root two over three squared times root two over three. I like to think that way because this works out to a nice two over three and then we have this root two over three remaining. So this over here is a way to explain where this came from. And now we have four times two is eight times root two and the denominator we have three, root three. So mg equals eight root two kqQ over three root three d squared. And our job is to solve for little q, we want to know what magnitude should the charge be on the corners of the square to make the mass get suspended in the center of the square. So we multiply both sides by three root three d squared over eight root two kQ, and that’s what happen in this line here, and also switch the sides around so we have the unknown on the left. So we have little q is three root three d squared mg, all over eight root two kQ. Now when you’re simplifying radicals, apparently you’re supposed to have the denominator with no square root in it, so we’re going to multiply this by one, but one is going to look like root two over root two so that there is no radical in the denominator. So in the bottom we get eight times root two squared which is eight times two which is 16, and then on top we have three root six. So little q is three root six, side length of the square squared times the mass that is suspended times gravitational field strength g, divided by 16 times Coulomb’s constant times the charge of the mass capital Q. Now this is an unstable equilibrium because if this charge was to move horizontally, then the horizontal component of the force from one corner would no longer equal the horizontal component of the force from the other corner, and well, actually, come to think of it. Maybe this is stable after all, come to think of it. Because, let’s erase some of these things here. If this thing was moved to the side, let’s say towards this corner, let’s say this corner here, then the x component of the force due to this charge would increase because the suspended charge is now closer to it. And that would result in a net horizontal force that would reverse the movement, so if it moved this way, it would experience a net horizontal force back to where it came from. And then if it went beyond, again on this side then it would experience a net horizontal force from this charge to which it is now closer here, that would restore it back to its original position. So I’m going to change what I thought before, and say that this is a stable equilibrium. Because movements horizontally will result in a force that restores the charge back to its original position. Bear with me as I change my mind. This is a stable equilibrium since movements horizontally would result in a net horizontal component to restore the original position. So there. Voila.
Comments
That just blew my brain open
I'm having trouble figuring out how simplifies to could you help?


