- The ratio of electrostatic force to the gravitational force for the electrons and protons is different since their masses are different.
Solution video
OpenStax College Physics, Chapter 18, Problem 21 (Problems & Exercises)

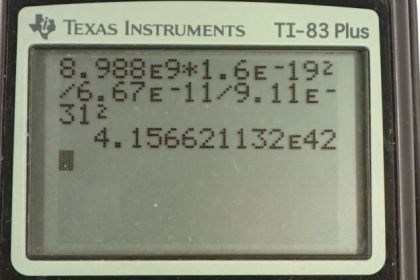
Calculator Screenshots
Comments
You divided the gravitational constant by the mass of the electron, instead of multiplying
Hi Devin,
Thank you for the comment. I think you're looking at the first calculator screenshot? I see what you mean - there's a "divide by the mass of the electron squared" following the gravitational constant. There isn't a mistake however - there's an issue of personal preference here about how to manage multiple factors in the denominator of a fraction. I'm guessing that your approach, which is totally fine, is to enclose the denominator in brackets, in which case you would need to see a multiply sign between the gravitational constant and the electron mass. My approach (which is no better, and in your case more confusing as it turns out, but I like it since there are fewer button pushes) is to not put brackets around the denominator. Without the brackets, since the calculator works from left to right, each division is dividing the result of everything before it. The division by the electron mass is dividing the result of the numerator after it has been divided by the gravitational constant. The electron mass is dividing the result of everything before it, not dividing the gravitational constant alone.
Hope this helps,
Shaun