Question
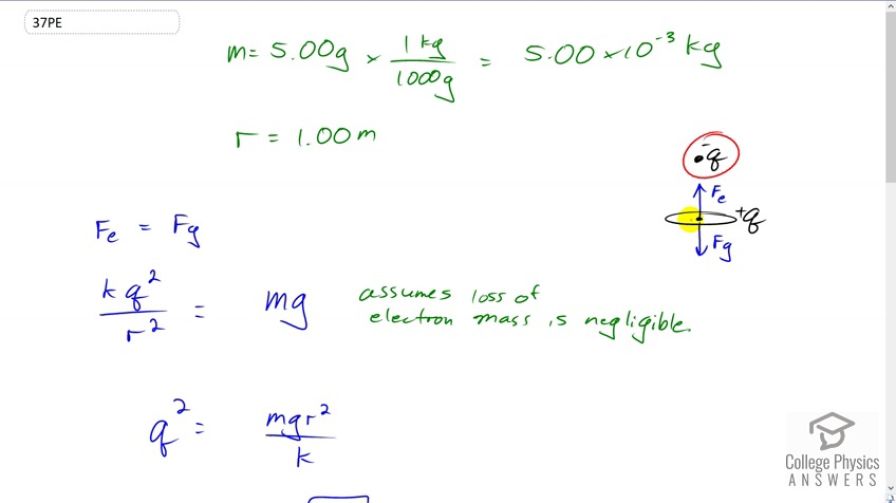
A certain five cent coin contains 5.00 g of nickel. What fraction of the nickel atoms' electrons, removed and placed 1.00 m above it, would support the weight of this coin? The atomic mass of nickel is 58.7, and each nickel atom contains 28 electrons and 28 protons.
Final Answer
Solution video
OpenStax College Physics, Chapter 18, Problem 23 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In this question we're going to have a nickel suspended in the air because of an electrostatic force upwards due to this charge that has been removed from the nickel and placed up here above it. We're going to have gravity downwards and these forces will be equal so that it is just suspended. Now the mass of the nickel we're told is five grams and we'll convert that into kilograms, and the distance between the charges that were removed and the nickel is one meter. So the electrostatic force has to equal the gravitational force. That means that Coulomb's times the charge squared, divided by r squared, has to equal m g. I can say charge squared because the amount of charge that's here was taken away from the nickel and so they're going to have equal magnitude charges but the nickel will be positive because it is missing this many electrons and this one is going to be negative because it consists of electrons. We can solve for q by multiplying both sides by r squared over k and we get q squared is m g r squared over k and then take the square root of both sides to solve for the amount of charge. This is going to give us an answer in coulombs which we'll then convert into number of electrons and then we'll take that as a ratio to the total number of electrons in the nickel to answer our question. So, the total number of electrons above the nickel, a for above, is this amount of charge q, times one electron for every elementary charge, we're converting this coulombs into a number of electrons. So substituting for q, we have r times square root m g over k, divided by q e is the number of electrons that have to be taken off the nickel and put above it. So that's one meter divided by the elementary charge, times square root of five grams, times 9.81 newtons per kilogram, divided by the Coulomb's constant. This gives 1.4601 times ten to the thirteen electrons. Now, what is that as a ratio of the total number of electrons in the nickel is the question. So the total number of electrons in the nickel we get by calculating -- well, we multiply the five grams by the molar mass written as one mole for every 58.7 grams, so now we have the number of moles in five grams, then we multiply by Avogadro's number, 6.02 times ten to the twenty-three atoms per mole, and now we have the number of atoms in the nickel, and then to figure out the number of electrons we need to know that its atomic number is 28, and so there are 28 electrons in every atom. We end up with 1.4358 times ten to the twenty-four electrons. So the ratio of the number above to the total number of electrons is this divided by that. You get 1.02 times ten to the minus eleven. So a very, very, very small fraction of electrons have to be removed in order to hold up the nickel. That's not a surprise because if you were following along in question thirty five, we saw that the ratio of electrostatic force to gravitational force is very large meaning the electrostatic force is much bigger than gravity, and so we would expect to not need very many electrons in order to provide an electrostatic force upwards that equals the gravity force downwards.

