Question
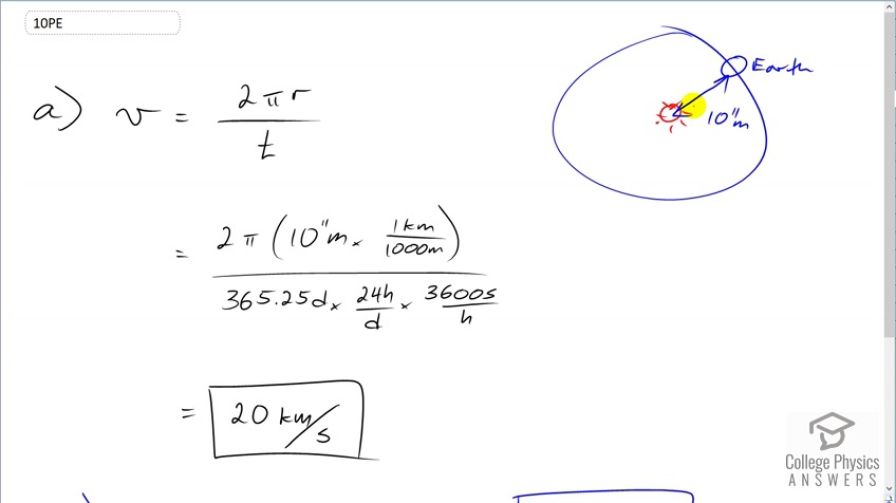
(a) Refer to Table 1.3 to determine the average distance between the Earth and the Sun. Then calculate the average speed of the Earth in its orbit in kilometers per second. (b) What is this in meters per second?
Final Answer
Solution video
OpenStax College Physics, Chapter 1, Problem 10 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
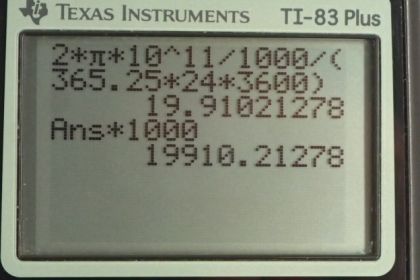
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to assume that the Earth approximately travels in a circle around the Sun and the Earth-Sun distance is going to be the radius of this circle and that is 10 to the 11 meters according to this table 1.3. So the speed of the Earth will be this distance which is the circumference of the circle and the formula for that is 2 times π times the radius of the circle divided by the time it takes to complete one circle which is 1 year. So we have 2π times 10 to the 11 meters expressed in kilometers because we are told to find our answer in units of kilometers per second in part (a). So we multiply by 1 kilometer for every 1000 meters giving us units of kilometers in the top here and then on the bottom, we divide by year but we have to express our year in seconds. So we have 365.25 days in a year times 24 hours per day which means the day units cancel but we are left with hours now and then multiply by 3600 seconds every hour and this gives us seconds; this works out to 20 kilometers per second and this number has one significant figure. And then in part (b) to express this in meters per second, we are going to review one good concept here which is to avoid intermediate rounding error. So when you use the result of one calculation in another calculation, you don't round the value when you are doing your next calculation. So instead of writing 20, I'm writing 19.910 kilometers per second and then we multiply that by 1000 meters for every kilometer—there— and the kilometers cancel giving us meters in our answer and so this is 2 times 10 to the 4 meters per second. And the reason we have only one significant figure for both here and here; I mean this is a little bit ambiguous one could claim that perhaps this zero is significant but I could have been more precise by writing 2 times 10 to the 1 kilometers per second that's possible to write it that way with scientific notation. We have only one significant figure because this distance here 10 to the 11 is the same as 1 times 10 to the 11 meters; this has one significant figure, there's very little precision involved in this measurement and so that's why we have only one significant figure in our answers here.
Comments
I am confused? Where did you get the km/second on part 2?
Hi sandeep, thank you for the question. Do you mean "where did 19.910 km/s" come from? It's the unrounded answer to part (a). Our job in part (b) is to convert the answer from part (a) into "meters per second". Calculations should always be done with unrounded values. Using rounded values in calculations is called intermediate rounding error, since it's an error to round an intermediate step of a larger calculation. Only final answers get rounded.
All the best,
Shaun