Question
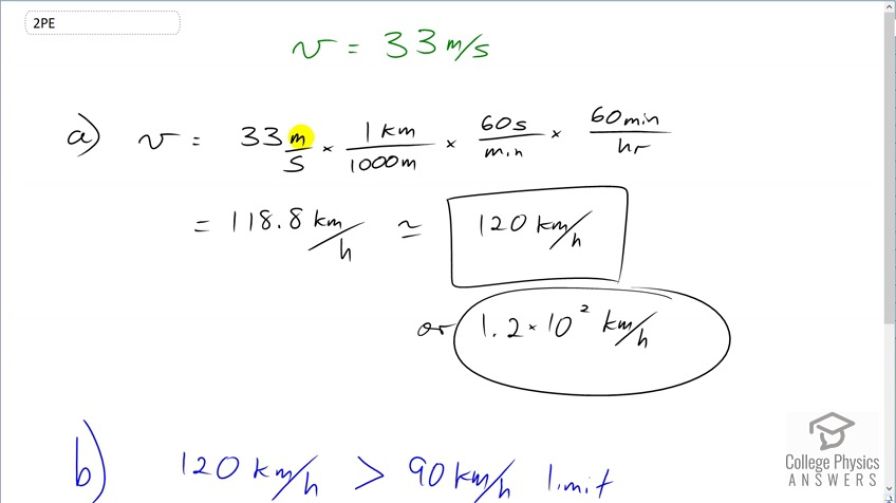
A car is traveling at a speed of 33 m/s. (a) What is its speed in kilometers per hour? (b) Is it exceeding the 90 km/h speed limit?
Final Answer
- or
- . Yes, this car is speeding.
Solution video
OpenStax College Physics, Chapter 1, Problem 2 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A car is traveling 33 meters per second and we are gonna convert that into kilometers per hour. So I write the units as a fraction m over s and then we want to create conversion factors that will cancel the units we don't want and leave us with units that we do want. So we want to get rid of the meters and replace it with kilometers and so meters is in the numerator of the units we are starting with and so we want meters to be in the denominator of our conversion factor and then we put the units that we do want on top which is kilometers. So we multiply by 1 kilometer for every 1000 meters and that means the meters cancel because they are being divided by each other and we are left with kilometers here so far. At this point, we have kilometers per second but now we want to get rid of the seconds units and replace it with hours. Now, if you don't have it memorized that there are 3600 seconds in an hour, you can instead do it step-by-step and say that there are 60 seconds per minute; this conversion factor has seconds in the numerator which is good because that will cancel with these seconds in the denominator but we are left with minutes on the bottom which is not good enough and we have to get rid of those and our next conversion factor has 60 minutes per hour; the minutes cancel leaving us with hours in the denominator. The only units left now are kilometers on top and hours on the bottom and that's what we want and so the arithmetic is 33 divided by a 1000 times 60 times 60 again. So that's 118.8 kilometers an hour but we have to keep in mind appropriate number of significant figures and this value that we start with has two significant figures and we are multiplying by all these conversion factors so our final answer has to have only two significant figures and so I write that as 120 kilometers per hour. Now this is a bit ambiguous because it's not clear whether there are two significant figures here or whether the zero is also significant. Now strictly speaking, this has two significant figures unless there was a decimal point here then there would be three but that's a really unusual way to write things. So this has two significant figures but to be absolutely clear, you could do scientific notation and write it as 1.2 times 10 to the 2 kilometers per hour. This speed of the car—120 kilometers an hour— exceeds 90 kilometers an hour and so yes, the car is speeding.


