Question
How many times longer than the mean life of an extremely unstable atomic nucleus is the lifetime of a human? (Hint: The lifetime of an unstable atomic nucleus is on the order of .)
Final Answer
Solution video
OpenStax College Physics, Chapter 1, Problem 31 (Problems & Exercises)
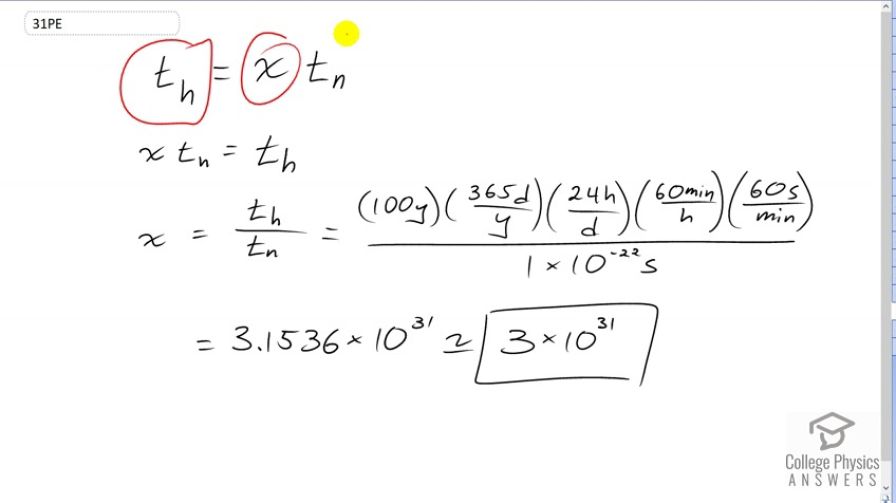
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko To calculate by what factor, the lifetime of a human is greater than the lifetime of an unstable atomic nucleus, we set the formula up like this. So, this is going to be the lifetime of a human and this will be the factor by which it's greater than this number here, being the time of the nucleus. Letter n for nucleus there, letter h for human. And we will isolate x after some algebra. We’ll switch the two sides of this formula around to get this line and then divide both sides by a lifetime of the nucleus and it cancels on the left isolating x there. And so, x is going to be this division of the lifetime of a human by the lifetime of the nucleus. Now, we need the units to be the same in the top and bottom, and for the lifetime of the nucleus, we’re given seconds. 1 times 10 to the minus 22 seconds. And so, we’ll convert our human lifetime into seconds as well, and we need to make some assumptions. And so, let's assume that a human lives for 100 years and we’ll multiply it by a bunch of conversion factors in order to turn that years unit into seconds. So, this is a 100 over 1, just like any number can be written over 1. In order to do that, in order to illustrate that this years is in the numerator. And so, it cancels with the years in the denominator of this conversion factor. And, so we’re multiplying 100 by 365 leaving us with units of days at this point, which we then multiply it by 24 hours per day and then times by 60 minutes per hour, then times by 60 seconds per minute, leaving us with seconds. And this works out to 3.1536 times 10 to the 31, but since we're dealing with very imprecise numbers that are just assumed, then we can't have much precision in our answer. And so, we’ll round that to one significant figure - 3 times 10 to the 31. You might get answers that are a little bit different, and that would be fine because you can make different assumptions about the lifetime of a human. Probably, 100 years is probably the maximum that one could assume. And so, you might assume something less and so you might have 2 times 10 to the 31 or 1 times 10 to 31. Any number with the same order of magnitude or to put out in other words, the same exponent for times 10 here would be acceptable.
