Question
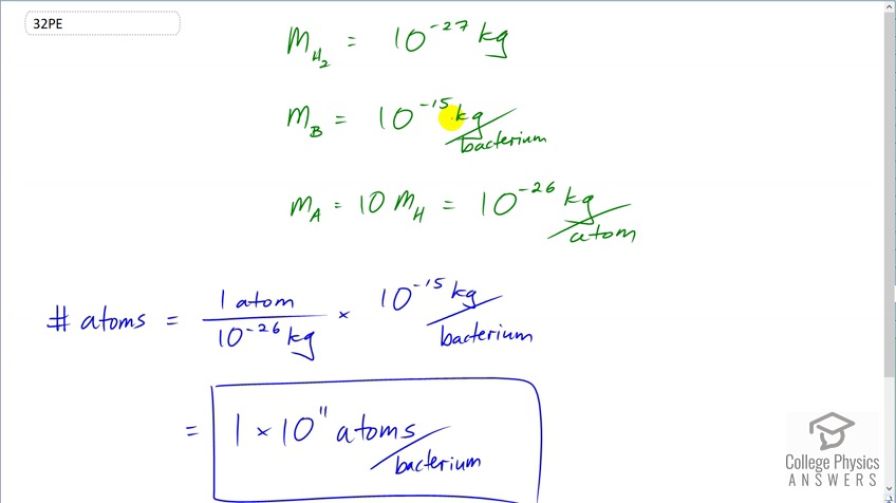
Calculate the approximate number of atoms in a bacterium. Assume that the average mass of an atom in the bacterium is ten times the mass of a hydrogen atom. (Hint: The mass of a hydrogen atom is on the order of and the mass of a bacterium is on the order of )
Final Answer
Solution video
OpenStax College Physics, Chapter 1, Problem 32 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to guess the number of atoms that are in a single bacterium and we are told that the mass of a bacterium is about 10 to the minus 15 kilograms and the average mass of an atom in a bacterium is 10 times the mass of a hydrogen atom and the mass of hydrogen atom is 10 to the minus 27 kilograms so 10 times that is 10 to the minus 26 kilograms per atom in the bacterium. So for the number of atoms in order to figure out how these factors should be set up, we want to have a factor that has the unit atoms in the numerator because atoms are what we want in our answer and so I'm writing this mass here as 1 atom for every 10 to the minus 26 kilograms and I knew to set it up that way because we want atoms in our answer. Then we have to multiply by kilograms to get rid of these kilograms in the denominator here so that's 10 to the minus 15 kilograms per bacterium and the kilograms cancel leaving us with atoms per bacterium which is what we want. And this works out to 1 times 10 to the 11 atoms per bacterium only one significant figure since all these estimates for masses here have one significant figure as well; if you see 10 to the minus 15, you can think of it as 1 times 10 to the minus 15. So this has one significant figure.
