Question
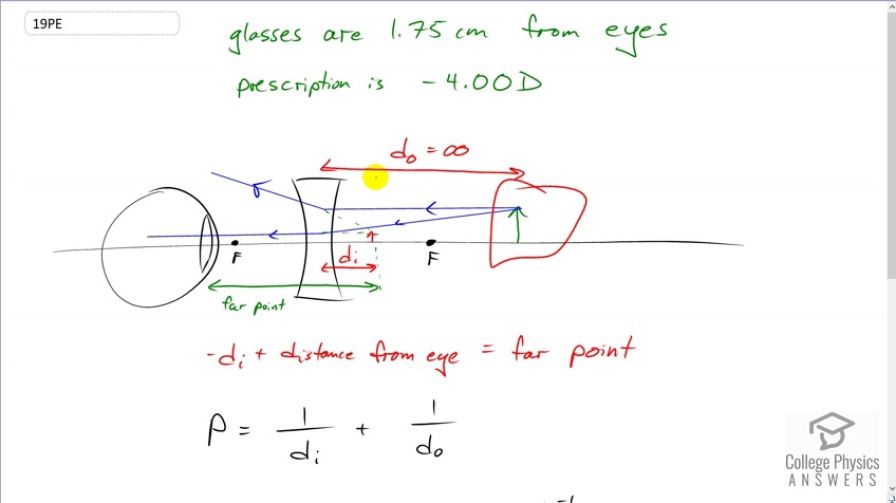
A myopic person sees that her eyeglasses perscription is -4.00 D, for eyeglasses positioned 1.75 cm from her eyes. What is her far point?
Final Answer
26.8 cm
Solution video
OpenStax College Physics, Chapter 26, Problem 19 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A person with myopia needs glasses to position an object which is at infinity at the far point of their eye when there are no glasses. So, the eye is able to see something that is this far away from it. Whereas, normally, with normal vision, you can see an object that is infinitely far away but with myopia, you need some glasses to bring that object closer to create an image of it which is closer so that your eyes can see it. So, we're going to figure out what this image distance is with respect to the lens and then add the distance between the lens and the eye to figure out what the far point is. So, the far point is this total distance between the lens of the eye and the location where the glass is positioned, the image of this object that's really far away. Okay. So this is the far point here that we're trying to figure out. And so, we'll add this 1.75 centimeters separation between the eye and the glasses. We'll add that to the image distance of the glasses and then get our answer for what is the far point. So, the power of the glasses is the reciprocal of this image distance plus the reciprocal of the object distance. But, the object is infinitely far away, so that makes this fraction zero. So, that's one divided by a really big number makes, essentially, zero. And so, we can take both sides to the exponent negative one here to solve for this image distance. And, it's going to be the reciprocal of the power so that's negative four diopters to the power negative one, which is negative 0.25 meters. And, it gets the negative sign because this is a virtual image, so for a lens, when the image is on the same side of the lens as the object, it is a virtual image. And so, the far point is going to be that distance with a negative in front of it, because we're just trying to take the absolute value of that distance, really, we want it to be positive. And, we'll add that to the separation between the eye and the glasses and we end up with 26.8 centimeters is the person's far point.
