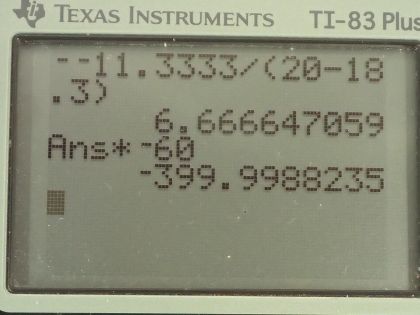
Question
An amoeba is 0.305 cm away from the 0.300 cm focal length objective lens of a microscope. (a) Where is the image formed by the objective lens? (b) What is this image’s magnification? (c) An eyepiece with a 2.00 cm focal length is placed 20.0 cm from the objective. Where is the final image? (d) What magnification is produced by the eyepiece? (e) What is the overall magnification? (See Figure 26.16.)
Final Answer
Solution video
OpenStax College Physics, Chapter 26, Problem 30 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
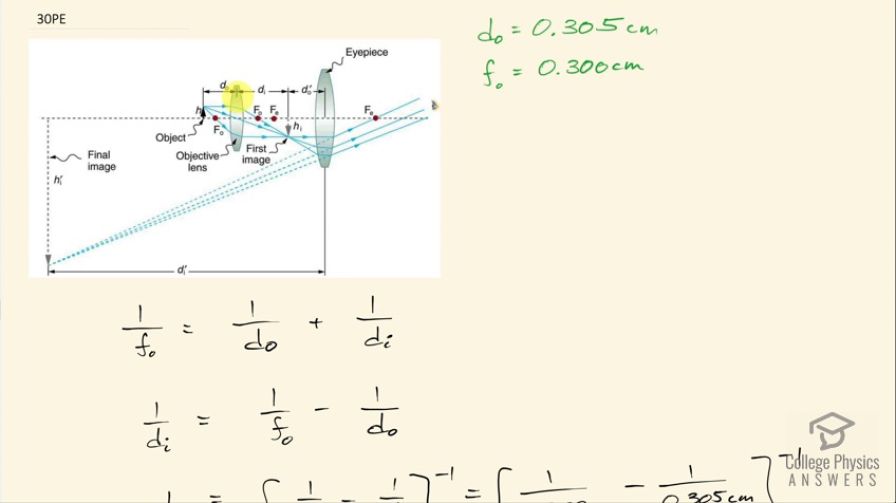
This is College Physics Answers with Shaun Dychko. An amoeba is placed 0.305 centimeters away from the objective lens of a compound microscope and the focal length of the objective lens is 0.300 centimeters and the question for part (a) is where is the image formed by the objective lens? So what is d i in other words? This distance from the objective lens to this image produced by the objective lens. The image that will be seen by the person looking through the eyepiece by the way will be this image here, the image produced by the eyepiece but first, we are taking things step by step here and first figuring out this image distance from the objective to this image here. So I am using the sin conventions from this figure [26.16] throughout my work here; d o is the object distance from the objective lens whereas d o prime—and 'prime' is the word for this little apostrophe— is the object distance from the eyepiece and d i is the image distance from the objective and d i prime is the image distance from the eyepiece. Okay! So for part (a), our job is to figure out d i— the image distance from the objective. So the thin lens equation says 1 over the objective focal length is 1 over d o plus 1 over d i— this is 1 over object distance plus 1 over image distance— we'll subtract 1 over d o from both sides and we get 1 over image distance then is 1 over objective focal length minus 1 over object distance. Raise both sides to the exponent negative 1 and you solve for the image distance. So that's going to be 1 over the objective focal length of 0.300 centimeters minus 1 over the object distance between the amoeba and the objective lens of 0.305 centimeters and then raise that difference to the exponent negative 1 and that gives 18.3 centimeters. Part (b) is asking what is the image's magnification? So the magnification of the objective lens is the negative of the image distance divided by the object distance. So that's negative of 18.3 centimeters divided by 0.305 centimeters, which is negative 60.0 times. Part (c) asks an eyepiece with a 2.00 centimeter focal length and so I am denoting the eyepiece focal length with a little subscript e on the focal length here— that's 2.00 centimeter focal length for the eyepiece— and this eyepiece is placed 20.0 centimeters from the objective so we need to understand that that is d i plus d o prime and we can see that by looking at this picture. So the eyepiece is placed 20.0 centimeters from the objective so its total distance is 20.0 centimeters and that is the total of the image distance between the objective and this real image here plus... this real image produced by the objective is the object for the eyepiece and so this distance between the eyepiece and this image from the objective is the object distance for the eyepiece labeled d o prime and this total d i plus d o prime is 20.0 centimeters so that's what I have written here. So we want to know where the final image is and that is d i prime—the image distance of the eyepiece. The thin lens equation for the eyepiece then is 1 over eyepiece focal length equals 1 over object distance prime plus 1 over image distance prime. The object distance prime is 20.0 centimeters minus the image distance from the objective—that's subtracting d i from both sides here— and we can substitute that in place of d o prime. So we have 20.0 centimeters minus d i in place of d o prime now and we will subtract this fraction from both sides subtract 1 over 20.0 centimeters minus d i and then we have 1 over d i prime isolated and it equals 1 over the focal length of the eyepiece minus 1 over 20.0 minus d i and then raise both sides to the exponent negative 1 to solve for d i prime and we have d i prime then is 1 over the eyepiece focal length minus 1 over 20.0 minus the objective image distance all to the negative 1. So that's 1 over 2.00 centimeters minus 1 over 20.0 centimeters minus 18.3 centimeters— that we calculated in part (a)— and then that is negative 11.3 centimeters. The negative sign says that we are working with a virtual image... it's only going to be on the same side as the eyepiece lens as the object is which is to say that if the object is on the left side of the eyepiece, the image also is on the left side of the eyepiece and it's this distance here as we expected from the picture. So part (d) is asking us what is the magnification produced by the eyepiece and that's going to be negative of the eyepiece image distance divided by the eyepiece object distance both labeled with a prime. So that's negative d i prime over 20.0 centimeters minus d i— we made that same substitution up here... from this— and that's negative of negative 11.3333 centimeters divided by 20.0 centimeters minus 18.3 centimeters and that's 6.67 magnification. The overall magnification then is the product of the magnification of the objective and the magnification of the eyepiece. So that's negative 60 multiplied by 6.67, which is negative 4.00 times 10 to the 2.