Question
A myopic person sees that her contact lens prescription is –4.00 D . What is her far point?
Final Answer
Solution video
OpenStax College Physics, Chapter 26, Problem 18 (Problems & Exercises)
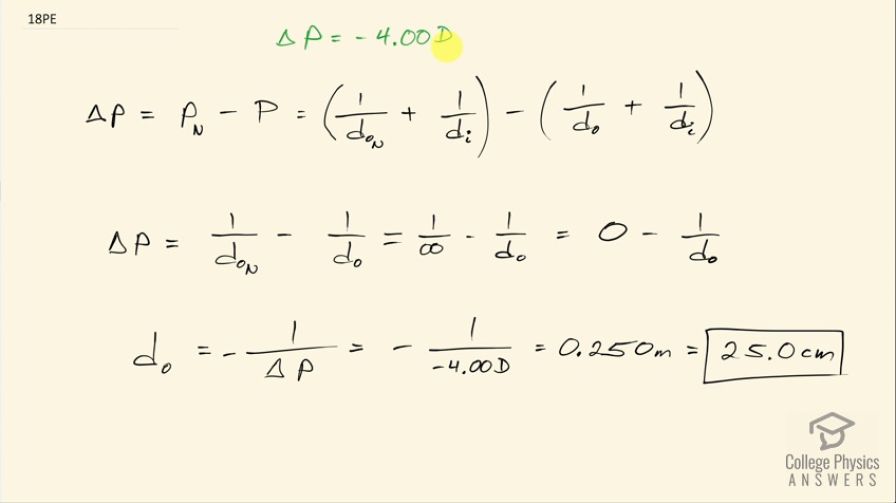
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This person has a contact lens prescription with a power of negative 4.00 diopters and the question is what is their far point without any contact lenses on? So their far point with the contact lenses will be infinity because that's the goal of the lenses is to create normal vision, which has a far point of infinity. So this change in power is the difference between the power for normal vision— looking at the far point— minus the power with no correction when looking at their far point and so this is 1 over the normal object distance of the far point which is infinity plus 1 over the image distance, which is the distance between the lens and the retina and then we'll subtract from that the power for uncorrected vision for this person, which is 1 over their far point which is what we have to find here plus 1 over the same image distance as before because this is a distance inside the eye between the lens and the retina. So this 1 over d i works out to zero here because it's plus 1 over d i minus positive 1 over d i and so this makes zero there and we are left with 1 over normal object distance in the far point minus 1 over object distance without correction. So the normal far point is infinity so this fraction is zero then and so we have a negative 1 over d o is ΔP. So negative 1 over their far point without correction is this correction provided by the contact lens. So we can raise both sides to exponent negative 1 and we have d o then is negative 1 over ΔP— I guess I multiplied both sides by negative 1 here too by the way to move the negative sign to the other side— so that's negative of 1 over negative 4.00 diopters which is positive 0.250 meters, which is 25.0 centimeters. So their far point is what a regular vision can see at its closest so this is as far away as they can see, it is 25.0 centimeters.
