Question
(a) What Hubble constant corresponds to an approximate age of the universe of ? To get an approximate value, assume the expansion rate is constant and calculate the speed at which two galaxies must move apart to be separated by 1 Mly (present average galactic separation) in a time of (b) Similarly, what Hubble constant corresponds to a universe approximately old?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 34, Problem 15 (Problems & Exercises)
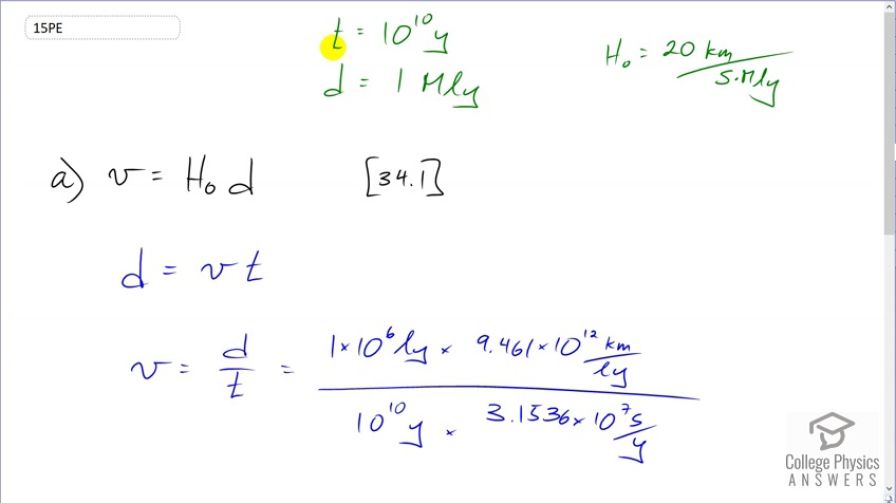
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
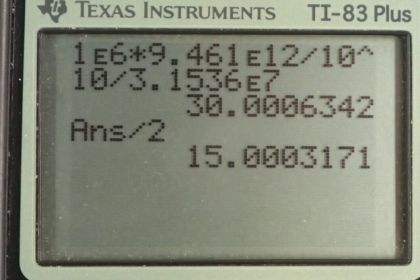
This is College Physics Answers with Shaun Dychko. We are going to calculate different values for the Hubble constant with different assumptions for the age of the universe. So in part (a), we'll assume the age of the universe is 10 to the power of 10 years and we'll figure out this H naught by finding the recessional speed of the galaxy that is 1 megalight years away and it's been moving away for this period of time. So equation 1 in chapter 34 says that the speed at which the galaxy is moving away is Hubble's constant times d. But we are going to find a different expression for that speed as well using this Kinematics formula, distance is speed times time and we'll divide both sides by t and we get v is distance over time and the distance we are told is 1 megalight year or 1 times 10 to the 6 light years and then we'll convert that into kilometers because the Hubble's constant has units of kilometers per second per megalight year and so we want to have our speed in kilometers per second in order to make the units that we are looking for. And then we are gonna divide that by a distance in megalight years. So we convert you know light years into kilometers by multiplying by 9.461 times 10 to the 12 kilometers for every light year and then we divide by the time which we assume is 10 to the 10 years and we have to convert that into seconds by multiplying by 3.1536 times 10 to the 7 seconds per year and this works out to 30.001 kilometers per second. So then Hubble's constant we get by you know, dividing both sides by d here. So Hubble's constant is the speed at which the galaxy is moving away divided by its distance so that's 30.001 kilometers per second divided by 1 megalight year giving a Hubble's constant of 30.0 kilometers per second per megalight year. So in part (b), we are told to assume a different time which is 2 times 10 to the 10 years. And so that makes it this new time— t prime—it makes it 2 times the time we were using before before we were using a time of 10 to the 10 or 1 times 10 to the 10 and now we have 2 times 10 to the 10 so that's a factor of 2 difference. And so we substitute 2t in place of t prime and this is v prime, the new speed of the galaxy receding given this new assumption of time. And this d over t is the v we had over here in part (a). And so when we calculate Hubble's constant in this new scenario, we have Hubble's constant prime is v prime over d and then we substitute v over d in place of or sorry v over 2 in place of v prime since it's v over 2 is v prime. And this v over d is the H naught that we had before and we are dividing it by 2 so 30 divided by 2 is 15. So this new Hubble's constant is given that the Earth or sorry the universe is 2 times 10 to the 10 years old, it's 15.0 kilometers per second per megalight year.