Question
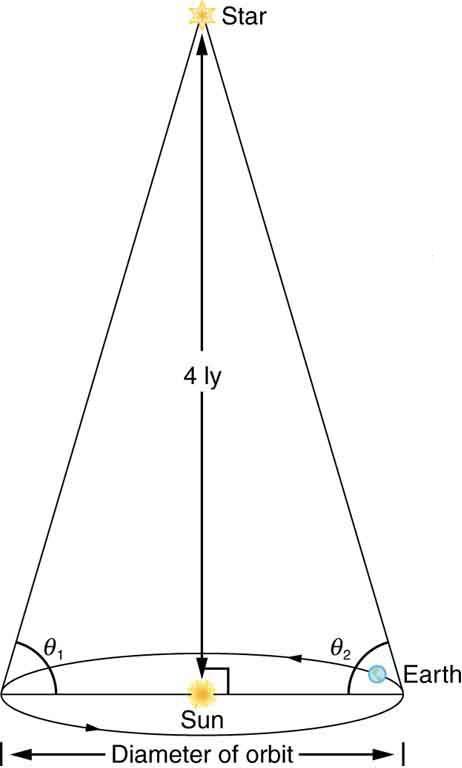
Distances to the nearest stars (up to 500 ly away) can be measured by a technique called parallax, as shown in Figure 34.26. What are the angles θ1\theta_1 and θ2\theta_2 relative to the plane of the Earth's orbit for a star 4.0 ly directly above the Sun?
<b>Figure 34.26</b> Distances to nearby stars are measured using triangulation, also called the parallax method. The angle of line of sight to the star is measured at intervals six months apart, and the distance is calculated by using the known diameter of the Earth's orbit. This can be done for stars up to about 500 ly away.
Figure 34.26 Distances to nearby stars are measured using triangulation, also called the parallax method. The angle of line of sight to the star is measured at intervals six months apart, and the distance is calculated by using the known diameter of the Earth's orbit. This can be done for stars up to about 500 ly away.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

90∘90^\circ or 89.99977∘89.99977^\circ if one has 7 significant figures in the measurements.

Solution video

OpenStax College Physics for AP® Courses, Chapter 34, Problem 19 (Problems & Exercises)

OpenStax College Physics, Chapter 34, Problem 19 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 34, Problem 19 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to measure this parallax angle between the Earth and this distant star which is 4 light years directly above the Sun and we can draw this triangle here where this leg is 4 light years; this leg is the Earth-Sun distance and this Θ 2 is the angle we want to find. Now the tangent of Θ 2 is going to be the opposite, which is 4 light years, divided by the adjacent which is the Earth-Sun distance and we can find the angle by taking the inverse tangent of both sides. So the angle is the inverse tangent of four light years converted into kilometers divided by the Earth-Sun distance in kilometers giving essentially 90 degrees to two significant figures or 89.99977 degrees.