Question
The characteristic length of entities in Superstring theory is approximately .
(a) Find the energy in GeV of a photon of this wavelength. (b) Compare this with the average particle energy of needed for unification of forces.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 34, Problem 26 (Problems & Exercises)
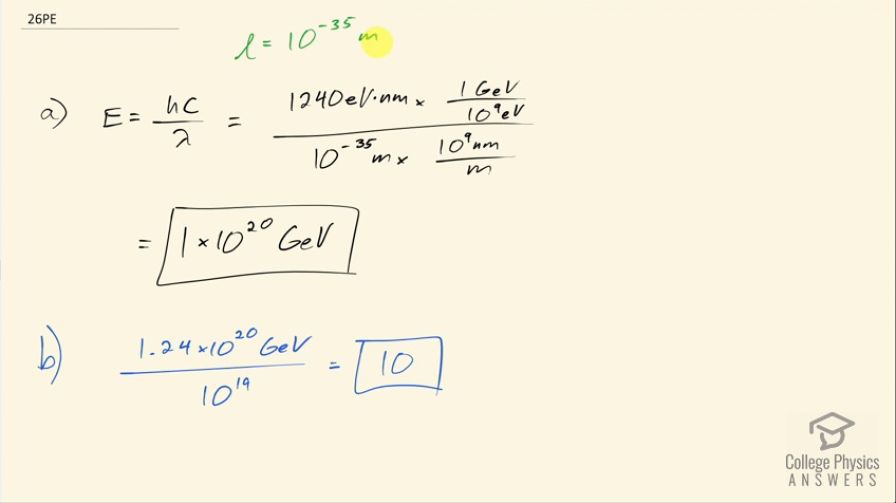
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The characteristic length of entities in Superstring theory is 10 to the minus 35 meters and if we imagine that a photon has this wavelength, what would its energy be? Well that would be Planck's constant times speed of light divided by the wavelength. We can write hc as 1240 electron volt nanometers and we want to convert this into gigaelectron volts we are told so we will convert this by multiplying by 1 gigaelectron volt for every 10 to the 9 electron volts and then the denominator has to be converted into nanometers to cancel with this nanometers in the unit here. So we have 10 to the minus 35 meters times 10 to the 9 nanometers per meter and we end up with 1 times 10 to the 20 gigaelectron volts. When we compare this with the average energy needed for the unification of forces, we divide that by 10 to the 19 gigaelectron volts and it is 10 times that energy.
