Question
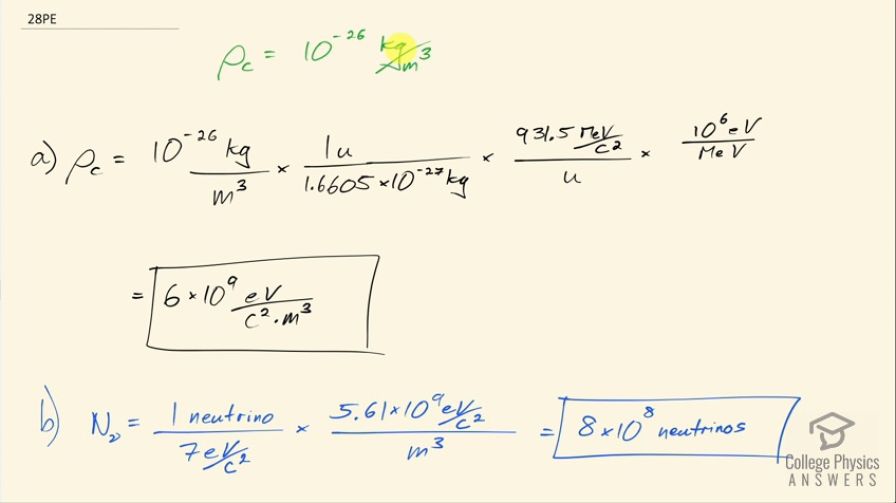
The critical mass density needed to just halt the expansion of the universe is approximately .
(a) Convert this to .
(b) Find the number of neutrinos per cubic meter needed to close the universe if their average mass is and they have negligible kinetic energies.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 34, Problem 28 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The critical mass density needed to stop the expansion of the universe is about 10 to the minus 26 kilograms per cubic meter. We will convert this into electron volts per c squared per cubic meter by multiplying 10 to the minus 26 kilograms per cubic meter by 1 atomic mass for every 1.6605 times 10 to the minus 27 kilograms and that gives atomic mass units per cubic meter and then convert the atomic mass units into megaelectron volts per c squared by multiplying by 931.5 megaelectron volts per c squared for every atomic mass unit and then convert this megaelectron volts into electron volts by multiplying by 10 to the 6 electron volts for every megaelectron volt. So now we have electron volts per c squared per cubic meter and that is 6 times 10 to the 9 electron volts per c squared per cubic meter. Part (b) asks how many neutrinos would you need to have this density? So it would be one neutrino for every 7 electron volts per c squared because we are told this is the supposed mass of a neutrino times 5.61 times 10 to the 9 electron volts per c squared for every cubic meter and this works out to 8 times 10 to the 8 neutrinos per cubic meter.