Question
The average particle energy needed to observe unification of forces is estimated to be . (a) What
is the rest mass in kilograms of a particle that has a rest mass of ? (b) How many times the mass of a hydrogen atom is this?
Final Answer
- times the mass of a hydrogen atom.
Solution video
OpenStax College Physics for AP® Courses, Chapter 34, Problem 13 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
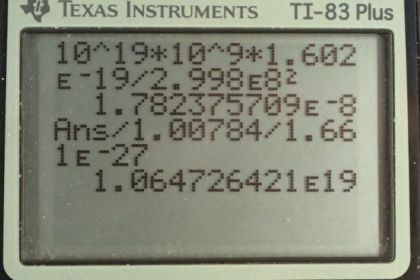
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We want to find the rest mass of a particle that has an energy of 10 to the 19 gigaelectron volts per c squared. So energy is mass times c squared and so we can divide both sides by c squared to solve for m. So we have 10 to the 19 gigaelectron volts per c squared and we are gonna convert this into joules by multiplying by 10 to the 9 electron volts per gigaelectron volt and then multiply by 1.602 times 10 to the minus 19 joules per electron volt; this gives joules per c squared then we divide that by the speed of light— 2.998 times 10 to the 8 meters per second for every c—and we square that and we get 2 times 10 to the minus 8 kilograms is the rest mass of a particle with this energy. And then the next question is what fraction or how many times is this mass of a hydrogen atom? So we take that mass and this is the unrounded value— 1.78 times 10 to the minus 8 kilograms— and we divide that by the mass of hydrogen which is 1.00784 atomic mass units for every hydrogen atom then we multiply that by 1.661 times 10 to the minus 27 kilograms per atomic mass unit and we are left with 1 times 10 to the 19. So this particle could be responsible for unifying all the four fundamental forces is 1 times 10 to the 19 times the mass of a hydrogen atom.