Question
Supermassive black holes are thought to exist at the center of many galaxies.
(a) What is the radius of such an object if it has a mass of Suns?
(b) What is this radius in light years?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 34, Problem 24 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
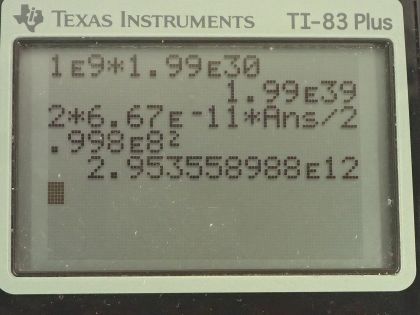
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. There is supposedly a super massive black hole at the center of many galaxies including ours and suppose a black hole has a mass of 10 to the 9 suns, what would its radius be? We will convert this into kilograms by multiplying by 1.99 times 10 to the 30 kilograms per Sun and that's 1.99 times 10 to the 39 kilograms. And the radius of a black hole is called the Schwarzschild radius and it's 2 times the gravitational constant times mass over speed of light squared. So that's 2 times 6.67 times 10 to the minus 11 Newton meters squared per kilogram squared times the mass divided by speed of light squared and that's 2.95 times 10 to the 12 meters. And that might seem like a big number but it's only about 10 times more than the distance between the Sun and the Earth. We are asked to figure out what is this distance in light years? So the first thing we should do is figure out how many meters a light year is. So we have the speed of light multiplied by a year that's converted into seconds and that's 9.46097 times 10 to the 15 meters per light year. So the number of light years then is the radius— our answer for part (a)— times 1 light year for every 9.46097 times 10 to the 15 meters which is 3.12 times 10 to the minus 4 light years.