Question
To get an idea of how empty deep space is on the average, perform the following calculations:
(a) Find the volume our Sun would occupy if it had an average density equal to the critical density of thought necessary to halt the expansion of the universe.
(b) Find the radius of a sphere of this volume in light years.
(c) What would this radius be if the density were that of
luminous matter, which is approximately 5% that of the
critical density?
(d) Compare the radius found in part (c) with the 4-ly average separation of stars in the arms of the Milky Way.
Final Answer
- The radius would be greater than the average stellar separation in the Milky Way by a factor of 300.
Solution video
OpenStax College Physics for AP® Courses, Chapter 34, Problem 30 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
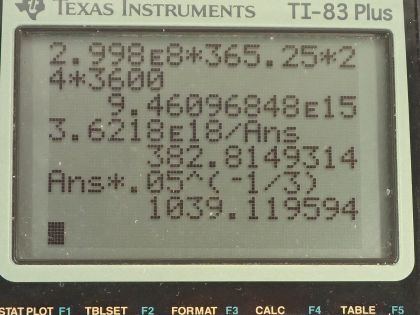
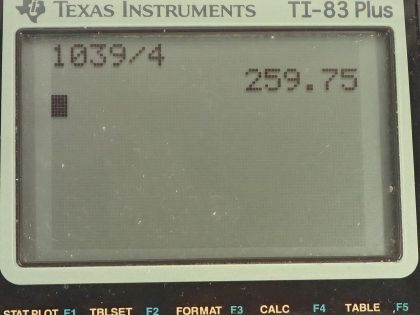
This is College Physics Answers with Shaun Dychko. To get an idea of how empty deep space is, we are going to find what volume our Sun would occupy if it had the density equal to the critical density thought necessary to stop the expansion of the Universe. So density is mass divided by volume and we can rearrange this to solve for volume by multiplying by V over ρ on both sides so volume then is mass divided by density. So that's 1.99 times 10 to the 30 kilograms— mass of the Sun— divided by the critical density of 10 to the minus 26 kilograms per cubic meter and that is 2 times 10 to the 56 cubic meters. Part (b) asks us to find the radius of a sphere that has this volume and express it in units of light years. So the volume of a sphere is four-thirds times π times radius cubed and we can solve for radius cubed by multiplying both sides by 3 over 4π. So radius cubed is 3 times volume divided by 4π and then we raise both sides to the exponent one-third to solve for r the radius. So the radius then is 3 times volume over 4π all to the power of one-third. So that's 3 times 1.99 times 10 to the 56 cubic meters— our answer from part (a)— divided by 4π all to the one-third, which is 3.6218 times 10 to the 18 meters. And then we will convert that into light years and first we need to know how many meters are in a light year. So light year is the distance that something traveling at the speed of light would go in one year. So that's 2.998 times 10 to the 8 meters per second— speed of light times a year—times 365.25 days per year times 24 hours per day times 3600 seconds per hour and that's 9.461 times 10 to the 15 meters. So this radius then is 3.6218 times 10 to the 18 meters times 1 light year for every 9.461 times 10 to the 15 meters and that's about 400 light years. Part (c) asks what would the radius be if the density was that of luminous matter, which is approximately 5 percent that of the critical density? So we could go through all these calculations again first finding the volume and then and then plugging that into our formula for the radius but instead we are going to take a little bit of a shortcut and see what factor we should multiply our answer from part (b) by in order to get our answer to part (c). So this new volume that we want to calculate—V 2— is mass divided by this new density and we are told that this density is 5 percent of the old critical density so that's 0.05 times the density we used before. So we have mass divided by the old density here, which we can replace with the old volume so the new volume then—V 2—is the old volume divided by 0.05. And our second radius then is going to be 3 times this new volume—V 2—over 4π all to the power of one-third but we can replace that V 2 now with V over 0.05 so we do that here and we see that we have 3 times the old volume over 4π to the power of one-third times 1 over 0.05 times to the one-third and this is the factor we want to multiply our old radius by to get our answer for this new radius so this gets replaced with the old radius. So we have 382.81 light years— that's expressing our answer for part (b) with more precision in order to avoid intermediate rounding error and we multiply that by 1 over 0.05 to the one-third, which is about 1000 light years. And part (d) says compare the radius we found in part (c) with the 4 light year average separation of stars in the arms of the Milky Way. So 1039 light years divided by 4 light years is about 300 so this radius would be greater than the average stellar separation in the Milky Way by a factor of about 300.