Question
Repeat Exercise 5.18 with the contestant pulling the block of ice with a rope over his shoulder at the same angle above the horizontal as shown in Figure 5.23 (b).
Exercise 5.18
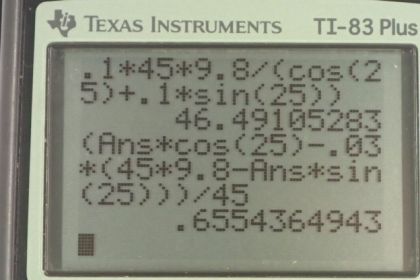
A contestant in a winter sporting event pushes a 45.0-kg block of ice across a frozen lake as shown in Figure 5.23(a). (a) Calculate the minimum force he must exert to get the block moving. (b) What is the magnitude of its acceleration once it starts to move, if that force is maintained?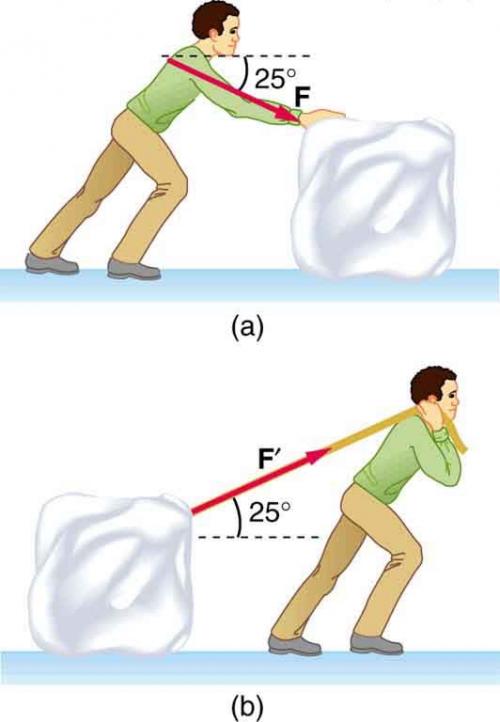
Final Answer
a)
b)
Solution video
OpenStax College Physics for AP® Courses, Chapter 5, Problem 19 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This person is going to be pulling a block of ice using a rope inclined above the horizontal at 25 degrees and this is going to cause a component of their force to be upwards and that’s going to reduce the amount of normal force required to balance gravity going down. And because normal force will be smaller than it was in this scenario here or even compared to the rope being straight horizontal, this means the friction is going to be smaller. So in part a, we’re asked to find what is the force that they would have to apply along the rope to just barely start the ice cube accelerating, and that will happen when the x component of their applied force, which is along here F prime x equals a friction force going backwards. Now the friction force is the coefficient of static friction, and it’s static friction because the block has not started moving yet, multiplied by normal force. When we consider the normal force, well we know that the total up forces have to equal the total down forces, so the normal force up is added to the y component of the person’s applied force Fy prime. We can solve this for normal force by adding or subtracting I should say, F prime y for both sides, and that gives this line here. We can make a substitution for F prime y as being F prime multiplied by sin theta because if you consider this triangle here, it’s a right triangle and F prime y is the opposite leg of that triangle so we multiply the hypotenuse F prime by the sine of theta, where theta is where I’ve labelled this angle 25 degrees there. So we also know that F prime x is F prime times cos theta because this is the adjacent leg of this triangle. So we take all of these things we’ve just figured out and plug it back in up here, F prime x we’re gonna substitute as being F prime cos theta here and then the force of friction, we know that it’s mu s times Fn, so we have the mu s here but the Fn we figured out is Fg times F prime minus sin theta. So we also make a substitution for mg in place for Fg and then multiply through by mu s. Our job in this equation here is to solve for F prime, what is the applied force. So we distribute the mu s into the bracket and then we want to collect the F prime terms in the same side so we’re going to add mu s F prime sine theta to both sides to get this next line, F prime cos theta plus F prime mu s sin theta equals mu s mg. Then factor out the common factor F prime to get this line here, F prime times cos theta plus mu s sin theta equals mu s mg. Then divide both sides by this bracket to get this line here which is the applied force is gonna be mu s times mg over cos theta plus mu s sin theta. Now it’s always good to do a reality check in your work. When you get an answer, you check to see whether it makes sense depending on what you know about the physical situation. So we know that if this angle theta was zero and the person is pulling straight horizontal, then in that case there will be no component of their pull which will be vertical and in which case the normal force would equal mg and in that case the friction force would equal the coefficient of friction multiplied by mg because that’s what Fn would be. Let’s see if that’s true based on our formula. If theta was zero, this term would be zero because sine of zero is zero, and this term would be one because cosine of zero is one, and so this whole denominator would be one, in which case F prime would equal mu s mg, which makes sense because the applied force in the case of theta being zero would equal mu s times the normal force which in that case would have been equal to gravity mg. So this formula does make sense, it reduces to give us something that we are familiar with in the case where theta is zero. Okay. But theta is not zero, so let’s plug in numbers and get our answer. We have 0.1 is the coefficient of static friction between ice on ice multiplied by 45 kilograms, mass of that block, times 9.8 newtons per kilogram divided by cosine of 25 degrees plus 0.1 times sin 25, giving us 46.5 newtons is the force that we have to apply. Now where the next part in part b asks us to find the acceleration of the block, assuming that this is the force that continues to be applied even after the block has started sliding. So this is the net force in the horizontal direction, the component of the applied force in the x direction minus the friction equals mass times acceleration. And we’ll divide both sides by m to get this line here, F prime x minus F friction divided by m is acceleration. Now F prime x, we already know is F prime times cos theta because it’s the adjacent leg of this yellow triangle. That’s the easy part. And then the friction though, we’ll figure it out based on what we have here, friction is mu s, which we’ve written here, times the normal force which is mg minus F prime sin theta where I’ve said mg in place of Fg, and so that’s mg minus F prime sin theta. So we plug in numbers to get our answer. That’s 46.49 newtons applied force times cos 25 minus 0.03, coefficient of kinetic friction between ice when the ice is actually sliding, times 45 kilograms times 9.8 newtons per kilogram minus 46.49 times sin 25, all divided by 45 kilograms, giving an acceleration of 0.656 meters per second squared.