Question
Calculate the maximum deceleration of a car that is heading down a slope (one that makes an angle of with the horizontal) under the following road conditions. You may assume that the weight of the car is evenly distributed on all four tires and that the coefficient of static friction is involved—that is, the tires are not allowed to slip during the deceleration. (Ignore rolling.) Calculate for a car: (a) On dry concrete. (b) On wet concrete. (c) On ice, assuming that , the same as for shoes on ice.
Final Answer
a)
b)
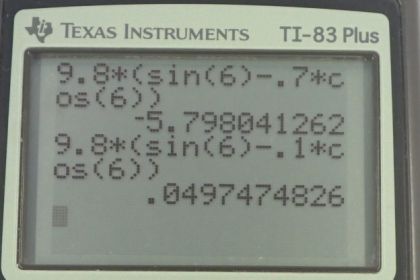
c) notice that this answer is a positive acceleration. The car is speeding up.
Solution video
OpenStax College Physics for AP® Courses, Chapter 5, Problem 13 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
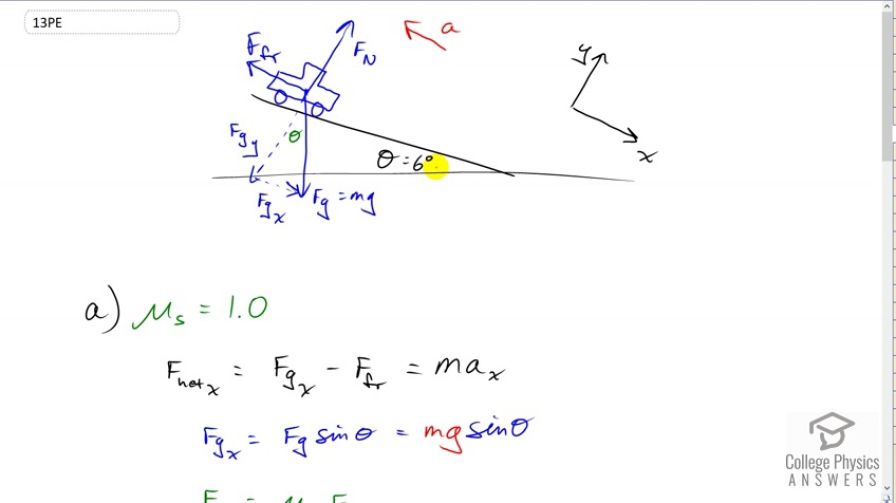
This is College Physics Answers with Shaun Dychko. In this question, we’re going to find the maximum deceleration that a car could have when it goes down this slope inclined at six degrees with three different surface conditions. In part a, we have rubber from the car tires on dry concrete for a coefficient of static friction of 1.0. Then in part b, it’ll be on wet concrete with a coefficient of static friction of 0.7. Then in part c, we assume the slope is icy with a static friction coefficient of 0.1. So we draw a free body diagram as we do for every question that we can in forces. I’ve rotated the coordinate system so that the x-axis is positive down the slope and the y-axis is perpendicular upwards and away from the slope. We expect a negative acceleration because the acceleration should be up the slope since we’re told the car is moving down and we want it to decelerate so that means acceleration is up the slope. This force of gravity needs to be resolved into two components, a component parallel to the slope and down which I call Fgx and then a component that is perpendicular to the slope Fgy. This angle in here is theta and we know that because this angle plus theta here adds up to 90 since this is a right triangle here with a right angle down there, since this gravity is straight down and this bottom line is straight horizontal. So this plus this angle has to make 90, and this plus this angle also has to make 90 since this Fgy is perpendicular to the slope. That means this angle here and the incline angle are the same, so that’s how we can say that this angle in this triangle here is theta. So the net force in the x direction is going to be positive Fgx down the slope and then minus force of friction up the slope. Let’s put the slope back. There. So this difference is the net force and so it is mass times acceleration, which I’ve labelled with a subscript x because it’s acceleration in the x direction. Now the Fgx is force of gravity times sin theta because Fgx is the opposite component of this blue triangle and so we multiply sin theta by the hypotenuse and the hypotenuse is force of gravity which is mg, so Fgx is mg sin theta. Then the force up the slope, friction, is the coefficient of static friction multiplied by the normal force. And so we can rewrite Fnet x as mg sin theta for Fgx and then minus mu k or mu s Fn substituted for force of friction, and all that equals ma x. Now the normal force is something we also need to substitute for, so we turn our attention to the y direction. In the y direction there’s no acceleration and so that’s why we can write zero there. Mass times acceleration is zero in that case because there’s no acceleration perpendicular to the slope, the acceleration is only along the slope. Having an acceleration perpendicular to the slope would mean the car would be flying or be buried in, going into a hole into the slope, which is not happening. So we can add Fgy to both sides here because we know the normal force is in the positive y direction and the Fgy is in the negative y direction so we have Fn minus Fgy there. So we add Fgy to both sides to solve for Fn and it’s going to equal the force of gravity y component and the force of gravity y component is mg times cos theta and it’s cosine because we’re finding the adjacent leg of this blue triangle, multiplying it by the hypotenuse. So we substitute Fn is mg cos theta in our net force in the x direction formula. So Fn becomes mg cos theta here, and so we have a formula for acceleration in the x direction now because we can divide both sides by m here, divided by m, divided by m, and the ms disappear. We have a x equals g which I factored out because it’s a common factor between these two terms. We have g times sin theta minus mu s cos theta. So there’s our formula that we can use to answer parts a, b and c. We just substitute different values for the coefficient of static friction in each case. So we have 9.8 meters per second squared times sine of six degrees minus one times cosine of six degrees, gives us negative 8.7 meters per second squared. We have the negative that we expected, that means acceleration is up the slope, the car will be slowing down because it is moving down the slope we’re told. Then in part b, we have 9.8 times sine of six minus 0.7 times cosine of six. 0.7 is the coefficient of static friction between rubber and wet concrete. And that is negative 5.8 meters per second squared is our maximum deceleration. Then if the slope is icy, we end up with 0.05 meters per second squared as our deceleration but we can’t really call it that because this is now positive. This means the car will be speeding up when it’s going down the slope, so when the car puts its brakes on, it will nevertheless continue to speed up. All it can do is minimize its acceleration, and so its minimum rate of speeding up will be 0.05 meters per second squared on an icy slope.