Question
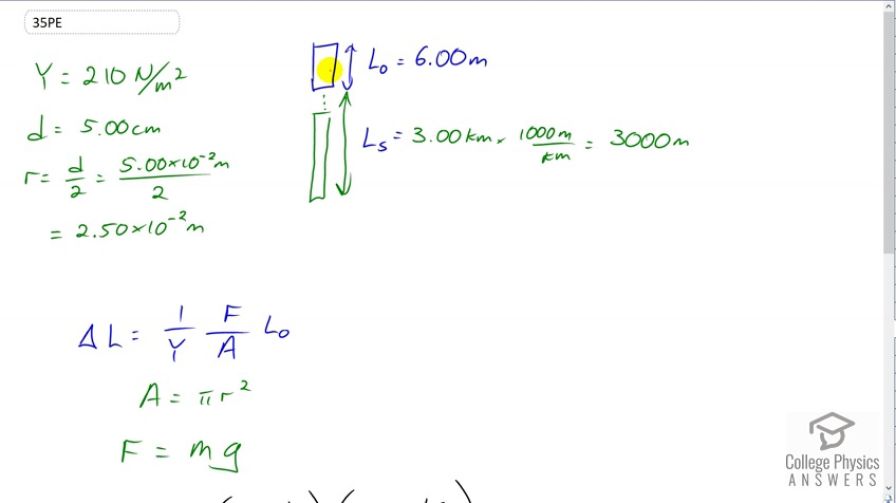
As an oil well is drilled, each new section of drill pipe supports its own weight and that of the pipe and drill bit beneath it. Calculate the stretch in a new 6.00 m length of steel pipe that supports 3.00 km of pipe having a mass of 20.0 kg/m and a 100-kg drill bit. The pipe is equivalent in strength to a solid cylinder 5.00 cm in diameter.
Final Answer
As pointed out in some perceptive comments below, the 100 km mass of the drill bit should be added to the mass of the 3 km of steel pipe. They are both being supported. As it turns out, including the drill bit mass won't change the answer to 2 significant figures since 100 kg is negligible in comparison to the 3 km of steel pipe, but nevertheless it's an unfortunate omission that the solution doesn't include the drill bit mass.
Solution video
OpenStax College Physics for AP® Courses, Chapter 5, Problem 35 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In this question we're going to find out by how much this oil well drill pipe is going to stretch. It has to support its own weight as well as the weight of all of the drill pipes sections below it and there are three kilometers of pipe below it and that works out to 3000 meters. We're going to start by just writing down the data we are given. So the Young Modulus is going to be 210 times ten to the nine newtons per square meter, that's the Young's Modulus for steel. The diameter of the pipe we're told is equivalent to 5 centimeters which we'll divide by two because we're going to need the radius in our calculation for the cross sectional area of the pipe. So we'll divide five times ten to the minus two meters taking care of the unit conversion of centimeters to meters there, divide that by two and that gives 2.5 times ten to the minus two meters radius. So, the change in length of the top piece of pipe is going to be one over Young's Modulus, multiplied by the force applied on it, which is going to be the weight of all the pipe below it, plus its own weight, divided by its cross sectional area, multiplied by its original length of 6 meters. So the area is pi r squared and the force that is applied on it pulling it down is going to be the total mass of all the pipe below it and its own mass times g. So the mass is going to be the total length of pipe, which is its own length plus all the length below it, multiplied by 20 kilograms per meter. So we plug in m here for the force and then that's multiplied by g so that's where this whole numerator here or the part of the numerator there, comes from. So that's the substitution for f. f is the m which is l naught plus l s times 20, multiplied by g. Then dividing that by area which is pi r squared, multiplied by the original length, and then divided by Young's Modulus. So that's one over 210 times ten to the nine newtons per meter squared, times 6 meters plus 3000 meters, times 20 kilograms per meter, times 9.8 newtons per kilogram, multiplied by 6 meters, divided by pi times 2.5 times ten to the minus two meters radius squared. This gives about 8.6 millimeters of stretch for the top section of pipe supporting three kilometers of pipe below it.
