Question
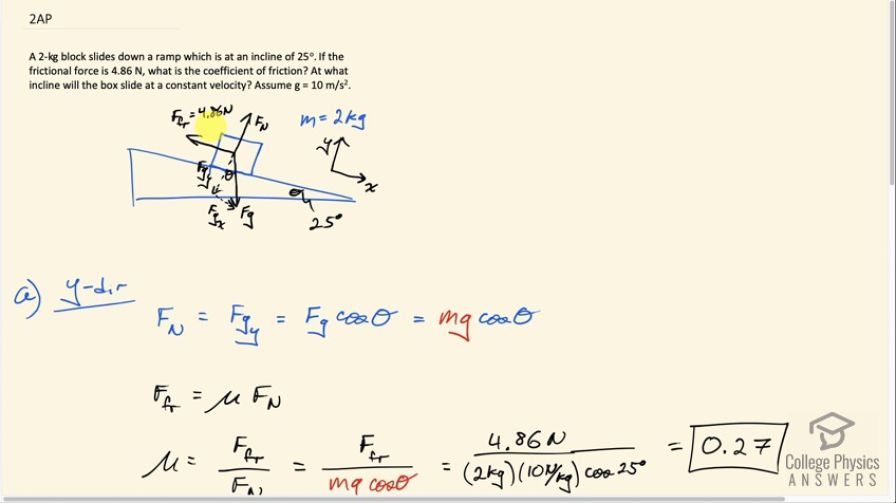
A 2-kg block slides down a ramp which is at an incline of . If the frictional force is 4.86 N, what is the coefficient of friction? At what incline will the box slide at a constant velocity? Assume .
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 5, Problem 2 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
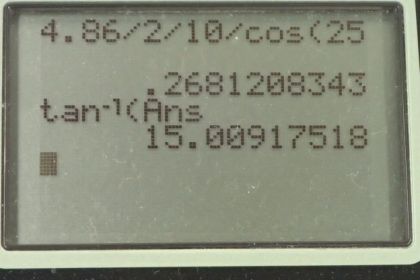
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A 2-kilogram block is sliding down a ramp that's inclined at 25 degrees and there's a friction force of 4.86 newtons. So this free-body diagram is helpful; we have a coordinate system that's been rotated so that the x-axis is down to the right along the ramp and the y-axis is perpendicular to the ramp and there's a force of gravity straight down which has perpendicular and parallel components: we'll call it F g y and F g x. This angle in here is Θ, the same as the incline angle, and this is a right triangle. Well, we are gonna figure out the answer to the first question: what's the coefficient of friction? So in the y-direction, we have this normal force equal to the y-component of gravity and that is gravity which is the hypotenuse of this triangle here multiplied by cosine of Θ because the y-component of gravity is the adjacent leg of this right triangle. So we have F g times cos Θ and F g is mass times acceleration due to gravity so we have mgcos Θ. So that's the normal force and the friction force is the coefficient of friction that we want to find multiplied by that normal force and we are given the friction force so we are gonna divide both sides by the normal force to solve for μ and then substitute mgcos Θ in place of the normal force. So we have the coefficient of friction then is the friction force divided by mgcos Θ. So that's 4.86 newtons divided by 2 kilograms times 10 newtons per kilogram times cos of 25 degrees which is 0.27. In the next part, we want to know at what incline angle will the box slide at constant velocity? So at constant velocity, we have the friction force up the ramp equal to the x-component of gravity down the ramp and the x-component of gravity is mg times sin of Θ because this x-component is the opposite leg of this triangle so we take sin of Θ multiplied by the hypotenuse to get this F g x and that has to equal the friction force upwards—upwards being up the ramp in this case. So the friction force is μ times F N— F N being mgcos Θ— so we have μmgcos Θ is the friction force and that's what I write here and F g x is mgsin Θ and then we solve this for μ by dividing both sides by mgcos Θ and then switch the sides around as well and then we end up with sin over cos equals the coefficient of friction and sin over cos is tangent of Θ and so we can solve for Θ then by taking the inverse tangent of both sides. Knowing that sin Θ over cos Θ is the same as tan Θ is a trigonometric identity that is worthwhile memorizing. So Θ is the inverse tangent of the coefficient of friction so it's the inverse tangent of 0.26812 which is 15 degrees.