Question
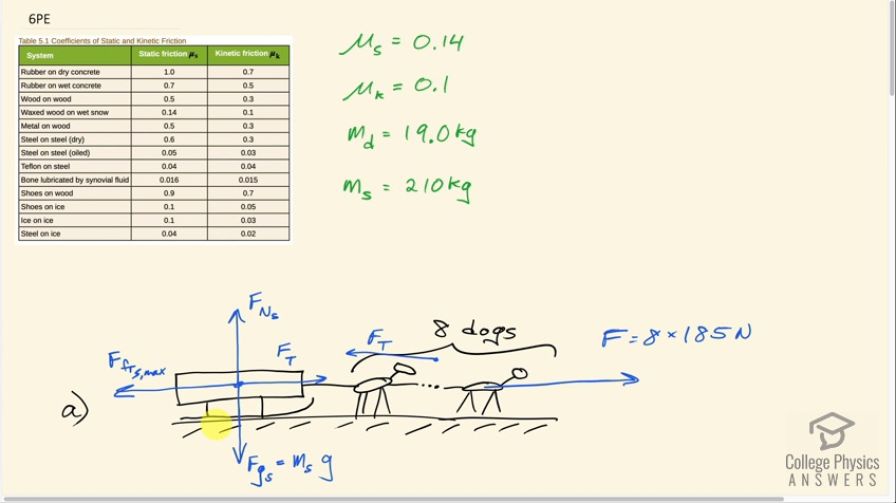
A team of eight dogs pulls a sled with waxed wood runners on wet snow (mush!). The dogs have average masses of 19.0 kg, and the loaded sled with its rider has a mass of 210 kg. (a) Calculate the magnitude of the acceleration starting from rest if each dog exerts an average force of 185 N backward on the snow. (b) What is the magnitude of the acceleration once the sled starts to move? (c) For both situations, calculate the magnitude of the force in the coupling between the dogs and the sled.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 5, Problem 6 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
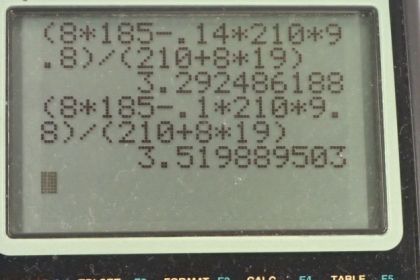
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a dog sled that has waxed skis on wet snow and these skis are made out of wood and so when we look in our table [5.1] for the coefficient's of friction, we can find waxed wood on wet snow and the static friction coefficient is 0.14 and the kinetic friction coefficient is 0.1 so we write down those pieces of information. We know that the mass of each dog is about 19 kilograms and the mass of this sled including the rider is 210 kilograms and here's our free-body diagram of the situation. We have eight dogs; they are each pushing on the ground with a force of 185 newtons on average so I could draw a vector here on the ground. This is a force on the ground due to the dogs and there's eight of them times 185 newtons per dog and that results in a force on the dog due to the ground— Newton's third law counterpart— and this is a force of static friction between the feet of the dogs which are not sliding and the wet snow. And there's also a static friction force going backwards on the sled runner's and we are interested in the case where the sled is just about to start moving and so at that point, the static friction force is at its maximum and so it's gonna equal the coefficient of static friction times the normal force. There's a normal force upwards on the sled and a force of gravity downwards on the sled and that force of gravity is gonna be the mass of the sled times g. So... well, we also have these tension forces here but these forces are internal to the system so they will be interesting when we get to part (c) when we have to find the force in this coupling between the dogs and the sled but on the system as a whole, these two forces are internal so they don't affect the overall system. It's just this force to the right on the dogs due to the ground and this force to the left which is on the sled that are important for calculating acceleration of the system. Okay! So the total force to the right—which I've just labeled F— minus the static friction force to the left, which is only on the sled, equals the total mass of the system which is the sled plus the eight dogs times the acceleration of the system. And this static friction, at its maximum, is the coefficient of static friction multiplied by the normal force on the sled and the normal force on the sled is the mass of the sled only times g. So we substitute this in place of the static friction force maximum pointing to the left here—and we do that in red here— and then we solve this for acceleration by dividing both sides by this total mass. So the acceleration then is gonna be the total force to the right minus the static friction coefficient times the mass of the sled times g all divided by the total mass. And so that's 8 times 185 newtons— exerted per dog— minus 0.14—static friction coefficient—times 210 kilograms—mass of the sled— times 9.80 meters per second squared divided by mass of the sled plus 8 dogs and that is 3.3 meters per second squared will be the acceleration at the very beginning when the sled just starts to move and we assume that the friction force is still static. In part (b), we now have the sled fully sliding and the coefficient is now gonna be that of kinetic friction and so the acceleration is all the same here except for 0.1 instead of 0.14. So this is the kinetic coefficient of friction and this works out to an acceleration of 3.5 meters per second squared. In part (c), we are asked what is the tension force or the force on this coupling in each of these scenarios: both in the first one when there's static friction involved and then in the second one when there's kinetic friction involved. So the force of tension in the static friction case is to the right on the sled and to the left, we have the maximum static friction force and that equals the mass of the sled times the acceleration and it's only the mass of the sled we are concerned with here because we have defined our system now to be only the sled and not including the dogs. Acceleration is the same as before because you know, the sled and the dogs are all accelerating together and if you consider just the sled on its own, this acceleration will still be the same. And we have to find the tension force so we add the static friction force at its maximum to both sides and then replace it with this expression here that we had before for the maximum static friction force. That is the coefficient of static friction times mass of the sled times g and we can factor out this mass of the sled from both of these terms and we have then that the tension force in the static friction scenario is mass of the sled times acceleration plus static coefficient times g. So that's 210 kilograms times 3.2925 meters per second squared using the unrounded answer for part (a) for the acceleration plus 0.14 times 9.80 meters per second squared. This works out to 980 newtons is the force in this coupling exerting to the right on the sled. When there's kinetic friction, the picture is the same except that this arrow should then be should now be force of friction kinetic. And so to the right, we have the tension force in the kinetic friction case minus the force of friction kinetic to the left equals the mass of the sled times acceleration and then we solve for this by adding the friction force to both sides and then replacing it with the coefficient of kinetic friction times the normal force which is equal to gravity on the sled— mass of the sled times g— factoring out mass of the sled just as we did before and we have the tension force then in the kinetic case is mass of the sled times acceleration plus coefficient of kinetic friction times g. So that's 210 kilograms times 3.5199 meters per second squared— acceleration when there's kinetic friction— plus 0.1 times 9.80 which is 940 newtons.