Question
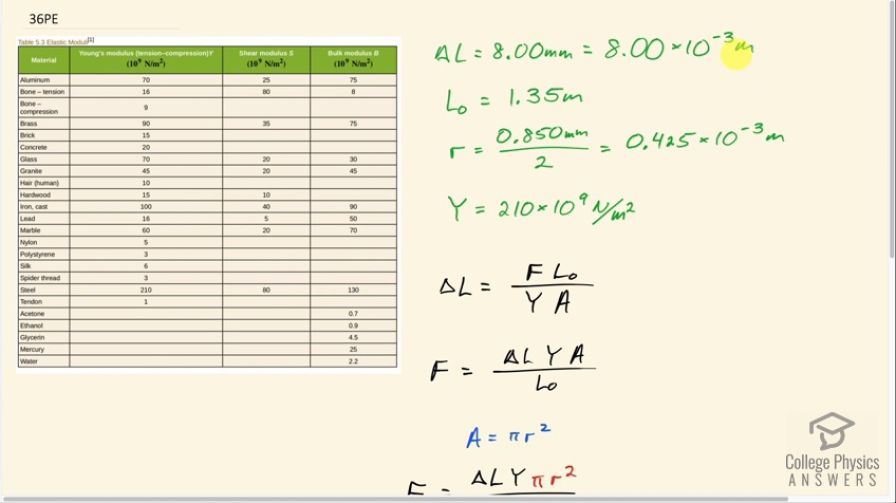
Calculate the force a piano tuner applies to stretch a steel piano wire 8.00 mm, if the wire is originally 0.850 mm in diameter and 1.35 m long.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 5, Problem 36 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A steel piano wire is being stretched 8 millimeters which we convert to 8.00 times 10 to the minus 3 meters. The original length of the piano wire is 1.35 meters and we are given the diameter of 0.850 millimeters but we want the radius because that's what we'll use for finding the cross-sectional area of the wire and the formula being πr squared for that. So we divide this diameter by 2 and then also take care of the unit conversion into meters so we have 0.425 times 10 to the minus 3 meters is the radius of the wire. The Young's modulus for steel we look up in table [5.3] and that is 210 times 10 to the 9 newtons per square meter and that's all the information we know and we'll turn to our formula here for the change in length under compression or tension for a material and it equals the tension force in this case times the original length divided by the Young's modulus times the cross-sectional area and we'll solve this for F by multiplying both sides by YA over L naught and then we get, after we switch the sides around, F equal to change in length times Young's modulus times cross-sectional area divided by original length and then we'll substitute πr squared in place of A. So we have the force then is 8.00 times 10 to the minus 3 meters— change in length— times 210 times 10 to the 9 newtons per square meter— Young's modulus for steel—times π times 0.425 times 10 to the minus 3 meters—radius—squared divided by 1.35 meters—original length— and that gives 706 newtons has to be applied by the piano tuner.
