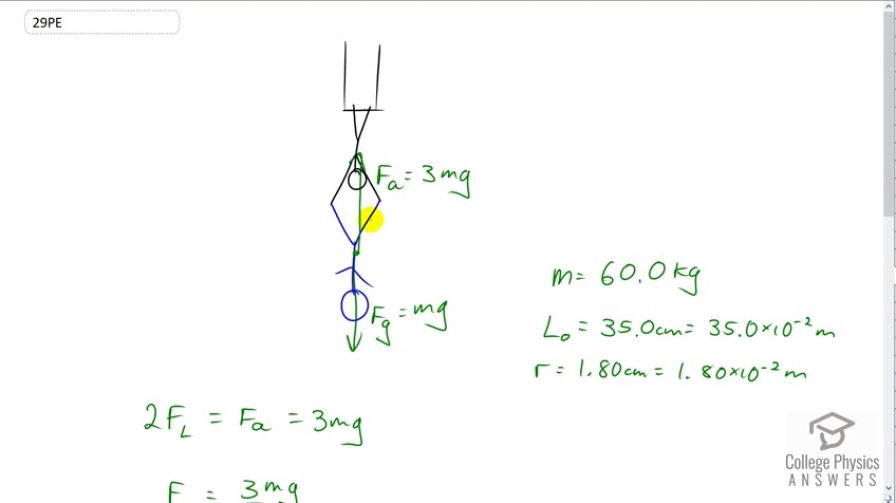
Question
During a circus act, one performer swings upside down hanging from a trapeze holding another, also upside-down, performer by the legs. If the upward force on the lower performer is three times her weight, how much do the bones (the femurs) in her upper legs stretch? You may assume each is equivalent to a uniform rod 35.0 cm long and 1.80 cm in radius. Her mass is 60.0 kg.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 5, Problem 29 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In this question we're going to calculate by how much the femur in this trapeze artiste's leg stretches when she's hanging upside down doing this acrobatic trick. So the total force applied upwards we're told is three times her weight. So that's three times mg and there's some other information which you just write down here. It's the trapeze artiste weighs 60 kilograms. The original length of her femur is 35 centimeters which is 35 times ten to the minus two meters, and the radius is 1.8 times ten to the minus two meters. So, always taking care of conversions of units and so on in this initial step when you're just writing down data from the question. So she has two femur bones, so two times the force on each leg is going to be the total applied force upwards which we're told is three times her weight. If we divide both sides by two here, we see that the force on a single leg is half of three times her weight or one and a half times mg. Now the change in length of her femur bone is going to be one over the Young's Modulus of bone when it's under tension, multiplied by the force applied to that leg, divided by its cross sectional area, multiplied by its original length. Its cross sectional area is going to be pi times the radius of the bone squared. So we make substitutions into delta l here. We have f l is three mg over two and then we have the area is pi r squared. So we have one over y times three mg over two times l naught over pi r squared is the change in length. So that is one over 16 times ten to the nine newtons per meter squared and this is the Young's Modulus for bone under tension when it's being stretched -- it's a different number if it was being compressed which is not the case here -- times three times sixty times 9.8 newtons per kilogram over two, times 35 times ten to the minus two meters, divided by pi times 1.8 times ten to the minus two meters radius squared, giving us a stretch of 1.9 times ten to the minus five meters, which about 20 micrometers which is a very small amount.
