Question
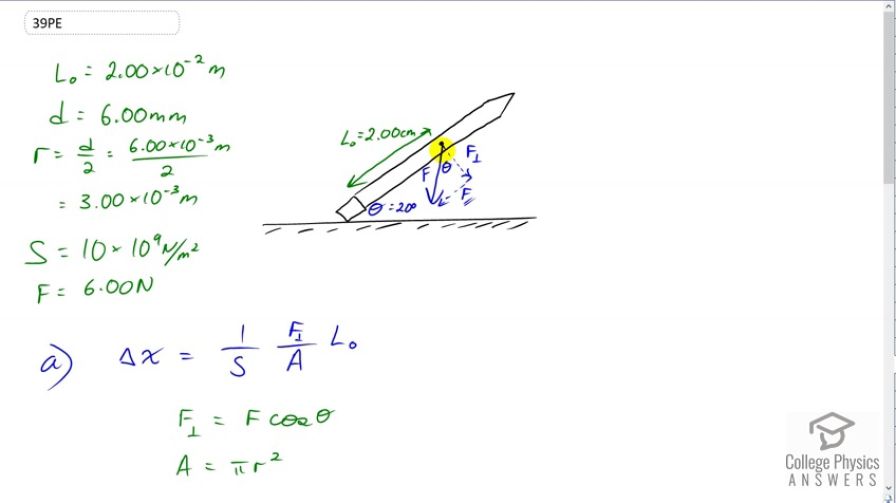
When using a pencil eraser, you exert a vertical force of 6.00 N at a distance of 2.00 cm from the hardwood-eraser joint. The pencil is 6.00 mm in diameter and is held at an angle of to the horizontal. (a) By how much does the wood flex perpendicular to its length? (b) How much is it compressed lengthwise?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 5, Problem 39 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
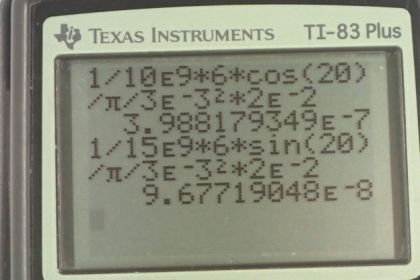
This is College Physics Answers with Shaun Dychko. So part A asks us to find out what is the shear deformation of this pencil because it's asking us how much does it bend perpendicular to its length. So this component of the applied force that is perpendicular to the length will be the shear force. Then we're asked to find out how much does this pencil shrink along its length and that'll be caused by the parallel component of the force. It's going to be compressed. We're told the force is applied straight down at a point two centimeters from where the eraser meets the wood of the pencil. The pencil is at an angle of 20 degrees above the horizontal. So in part A, we start with the formula for shear deformation, that's one over the Shear Modulus of wood, times the perpendicular component of the applied force, divided by the cross sectional area of the pencil, and times by its length between the point where the force is applied and where it's touching or where it's attached to the eraser. So we have all the data written down here which is a good way to start every problem, write down data, draw a picture. So the length is two centimeters which you convert into meters. The radius is something we want to know to find the cross sectional area because our formula for area is pi times radius squared. So we're given the diameter of six millimeters and so we divide that by two to get the radius and then also convert it into meters. We have three times ten to the minus three meters radius. The Shear Modulus of wood is ten times ten to the nine newtons per square meter and the force applied is six newtons. So after substituting for the area and also substituting for the perpendicular component of the force as force times cosine of the angle with respect to the horizontal, we get this formula here. The reason we have cosine is because if you think about this triangle here in yellow, it's a right triangle where there's a right angle down here and this angle up in here plus theta have to add up to 90 because the interior angles of a triangle total 180. 90 is taken up there which means there is 90 degrees left over for these two angles, so this dot plus this theta have to make 90. This dot plus this angle in here also has to make 90 because this is the perpendicular component of the force. So because the dot plus this angle in here makes 90 and the dot plus this angle down here also makes 90, that means that this angle is theta in here as I've labeled it. Okay. So the perpendicular component of the force is the adjacent leg of this triangle in blue. So we use cosine times the hypotenuse to get the adjacent leg. Then it's a matter of plugging in numbers. One over the shear modulus ten times ten to the nine newtons per square meter, times six newtons, times cos 20 divided by pi, times three times ten to the minus three meters squared, times two times ten to the minus two meters length of the pencil. That gives four times ten to the minus seven meters is the shear deformation. So it hardly bends at all. Then the amount that the pencil is compressed is the next question. So that's going to be one divided by the Young's modulus, multiplied by the parallel component of the force, divided by the cross sectional area of the pencil times its length. The parallel component is the force multiplied by sine theta because we're now finding the opposite leg of this triangle. We plug in pi r squared for area again, and we have one over 15 times ten to the nine newtons per square meter, Young's Modulus of wood, times six times sine 20 over pi times three times ten to the minus three squared, times two times ten to the minus two meters, giving us 9.7 times ten to the minus eight meters is the change in length of the pencil.