Question
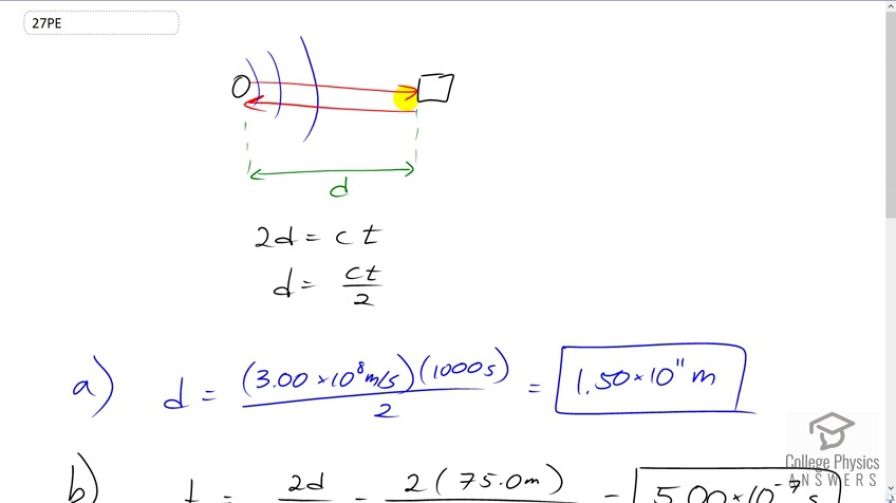
Radar is used to determine distances to various objects by measuring the round-trip time for an echo from the object. (a) How far away is the planet Venus if the echo time is 1000 s? (b) What is the echo time for a car 75.0 m from a Highway Police radar unit? (c) How accurately (in nanoseconds) must you be able to measure the echo time to an airplane 12.0 km away to determine its distance within 10.0 m?
Final Answer
Solution video
OpenStax College Physics, Chapter 24, Problem 27 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
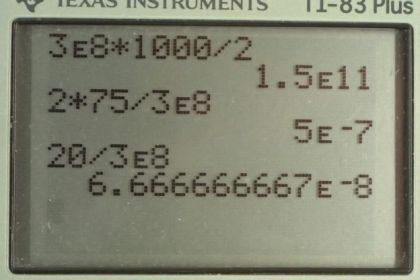
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When radar is measuring the distance to something, its emitting some EM radio waves which then bounce off the object and then return back to the radar and so these electromagnetic waves make a trip twice. There is a round trip that covers this distance between the radar and the object two times, and so we have two times the distance is equal to the speed that the wave is traveling multiplied by the total time for the round trip and so we can solve for d by dividing both sides by two, we get d is speed of light times time over two. So, assuming the radar takes 1000 seconds to do a round trip from Earth to Venus, we multiply that by three times ten to the eight meter per second divided by two and we get the distance from Earth to Venus is 1.50 times ten to the 11 meters and the time for reflection to a car that’s 75 meters away, or we can re-arrange this to solve for t, instead of dividing both sides by two, we could instead divide both sides by c and then that would gives us a formula for t. So, its two times distance over c. So, that’s two times 75 meters divided by three times ten to the eight meter per second, which gives a time of five times ten to the minus seven seconds or 50 micro-seconds. Part C says, assuming a plane is 12 kilo-metres away, what accuracy would your… your time measurement needs to be for the times of the round trip of the radar light. What accuracy would that need to be to get the distance to the airplane within ten meters. So that means it can plus or minus five meters. So, here is the time for… if the plane is plus five meters away, five meters more than 12 kilo-metres and here is the time if its five meters closer than 12 kilo-metres and we have two times distance divided by speed of light here. So, we are using this formula and plug in numbers from this question part C here and so that’s… when… since these have common denominator c we can add the numerators or subtract them as it the case is here, and so we have two times 12 times ten to the three minus two times 12 times ten to the three, so those make zero. So, we have two times five and then minus two times negative five which is a plus and so we have 20 meters over c and that works out to 66.7 Nano-seconds. So, this needs to be the minimum time resolution of the electronics in... that is detecting the time for the radar to do a round trip.