Question
Police radar determines the speed of motor vehicles using the same Doppler-shift technique employed for ultrasound in medical diagnostics. Beats are produced by mixing the double Doppler-shifted echo with the original frequency. If microwaves are used and a beat frequency of 150 Hz is produced, what is the speed of the vehicle? (Assume the same Doppler-shift formulas are valid with the speed of sound replaced by the speed of light.)
Final Answer
Solution video
OpenStax College Physics, Chapter 24, Problem 41 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
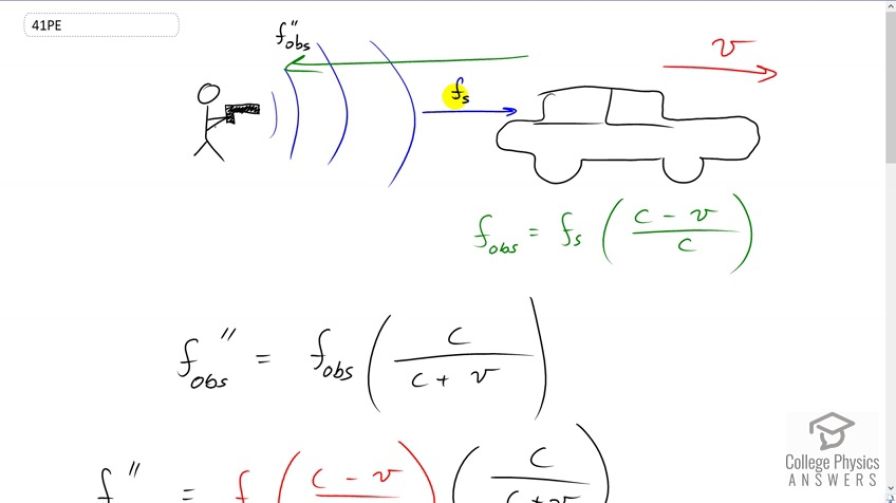
This is College Physics Answers with Shaun Dychko. This police officer who is standing still has a radar gun and the radar gun emits a certain frequency, we call it f subscript ‘s’ for source and this light basically is an electromagnetic wave so it’s a type of light, it hits the car and the car is moving away from the police officer and so the frequency that the car sort of perceives hitting it is not f s, it’s gonna be a Doppler Shift. So, this is the formula for Doppler Shift when the observer which is the car moving away from the source and so the frequency of the car sense it hitting it from the police officer is f obs, ‘obs’ for observer and that equals the frequency of the source being emitted by the radar gun multiplied by the speed of the wave which in this case is c because the wave is a light wave minus the speed of the car divided by c and then this frequency is going to get reflected from the car and notice that I wrote f double prime ‘obs’ here and so that’s… that’s not this frequency here because there is a Doppler Shift in the reflected frequency as well because the source is moving and the source being the car at this point so there are two Doppler Shifts happening. So, there is the frequency emitted hits the car and the frequency that the car senses it hitting it will be Doppler Shifted because the car being the observer moving away from the source and then further more when the car is reflecting the frequency, that is going to be Doppler Shifted as well because now we can think of this car as being the source and it is moving away from observer and so this is the formula for the Doppler Shifted frequency when we have a source moving away from the observer and the frequency that I have put in here, this would normally be f s in your Doppler Shift formula but I have f obs for the frequency that is observed by the car coming from the police officer and so we are gonna substitute for this with all of this and that’s we do in the second line here. So, the frequency that would be detected by the police officer, that’s what this one represents is going to be the Doppler Shifted frequency that the car detects hitting it And then which is in turn Doppler Shifted due to the car moving away from the observer which is a police officer. Okay. So, we have a bunch of algebra to do now to solve for v. The c (s) cancel here which is nice and we end up with this line of the frequency detected by the police observer is going to be the frequency that the police officer’s radar gun originally emits that’s f subscript ‘s’ times speed of light minus speed of the car divided by speed of the light plus speed of the car and now lets tie this up into the beat frequency that we are given. So, information we are given is that the beat frequency is 150 hertz and the original frequency is emitted by the radar gun is 1.50 times ten to the nine hertz and so beat frequency is the difference in the two frequencies and so the electronics in the radar gun knows what the frequency that was originally emitted and that is f s and… and then the difference between that and what is detected coming from the car I the beat frequency and so we substitute f s times c minus v over c plus v, in place of f observed double prime here and so this equation is what we will solve for v. So, lets multiply both sides by c plus v, to get rid of denominator there and so we have beat frequency times c plus v equals frequency of the source multiplied by the brackets c plus v minus this term multiplied by c plus v in which case it cancels there, sort of f s times c minus v and then distribute into each of the bracket there so we have beat frequency times speed of light plus beat frequency times speed of the car equals the source frequency times speed of light plus the source frequency times speed of car minus the source frequency times speed of the light plus, because this is a minus and a minus, plus source frequency times speed of the car. and some nice things happen here. This one and this one makes zero because the terms are same with opposite signs and these two term are the same with the same signs and so we have two times source frequency times speed of the car and then on the left side there is nothing to collect. So, we just have f b c plus f b v and then we will collect the term with the factor v in them on the same side and so we will subtract f b v from both sides and then switch the sides around so that unknowns are on the left and we factor out this common factor v among these two terms. So, a v times two f s minus f b equals f b c and then we divide both sides by two f s minus f b and we get our final formula. So, speed of the car is beat frequency times the speed of light divided by two times the frequency originally emitted minus the beat frequency. So, that’s 150 hertz beat frequency times three times ten to the eight meters per second divided by two times 1.50 times ten to the nine hertz, emitted by the radar gun minus 150 hertz which gives 15.0 meter per seconds is the speed of the car.
