Question
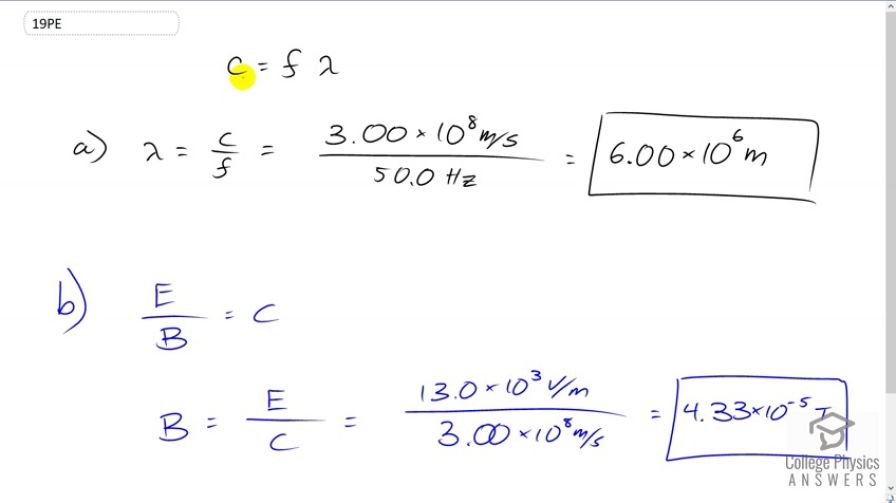
A certain 50.0-Hz AC power line radiates an electromagnetic wave having a maximum electric field strength of 13.0 kV/m. (a) What is the wavelength of this very low frequency electromagnetic wave? (b) What is its maximum magnetic field strength?
Final Answer
Solution video
OpenStax College Physics, Chapter 24, Problem 19 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to calculate the wavelength of the light emitted by this power line by using the wave equation, which says, the speed of a wave, which in this case is light and so we write c for the speed equals the frequency of the light times its wavelength and we'll divide both sides by f to solve for lambda. So we have the wavelength is a speed of light 3 times 10 to the 8 meters per second divided by the frequency of 50 hertz, which is 6 times 10 to the 6 meters. In Part b, we calculate the magnetic field strength of this electromagnetic radiation and we know that the ratio of electric field strength to magnetic field strength equals c and so we'll solve for B by multiplying both sides by B over c and then we'll also switch the sides around. So we have magnetic field strength is the maximum electric field strength, which is 13 times 10 to the 3 volts per meter divided by the speed of light which is 3 times 10 to the 8 meters per second giving a maximum magnetic field strength of 4.33 times 10 to the minus 5 Tesla.
