Question
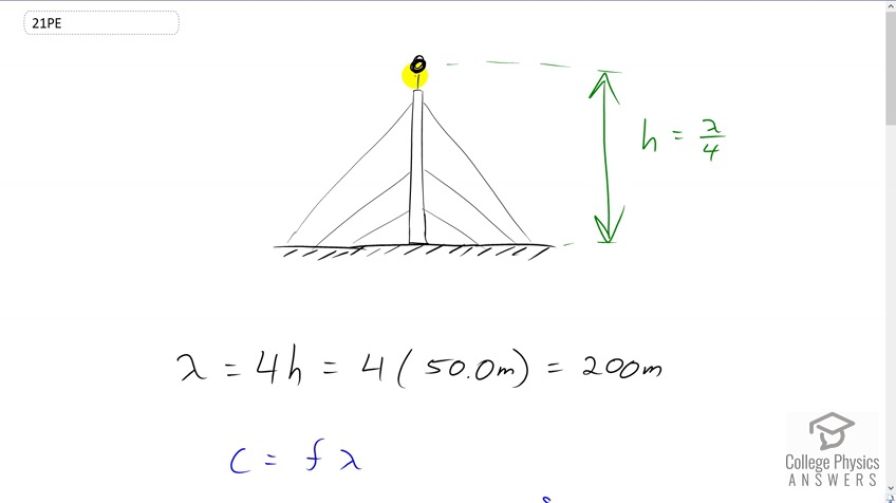
(a) The ideal size (most efficient) for a broadcast antenna with one end on the ground is one-fourth the wavelength () of the electromagnetic radiation being sent out. If a new radio station has such an antenna that is 50.0 m high, what frequency does it broadcast most efficiently? Is this in the AM or FM band? (b) Discuss the analogy of the fundamental resonant mode of an air column closed at one end to the resonance of currents on an antenna that is one- fourth their wavelength.
Final Answer
- . This is in the AM band.
- Resonance for an electromagnetic wave at is analogous to sound resonance in a closed end tube which also has . is analogous to . Further resonances for the antenna might occur at
Solution video
OpenStax College Physics, Chapter 24, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A broadcast antenna has a height which is one quarter of the wavelength of the electromagnetic radiation it's most efficiently emitting and so it will be built such that whatever wavelength its meant to broadcast is going to be… umm… four times its height or its height would be one quarter of the times of wavelength whichever way you want to look at it. So, yeah, wavelength is 4 times the height. So, that’s four times 50 meters and that makes 200 meters and then we can calculate its frequency using the wave equation which says the speed of the wave equals its frequency times the wavelength and we will solve for f by dividing both sides by lambda. So, f is the speed of light divided by lambda which is 3 times 10 to the 8 meters per second over 200 meters and that makes a frequency of 1.50 times 10 to the 6 hertz. This frequency is 1500 kilo-hertz which is in the AM band and what we are seeing here with this height of the broadcast antenna being related to the resonant wavelength that it is emitting is analogous to tube full of air closed at one end and in this case the length will equal the first resonant frequency over 4 in which case lambda one equals 4 times L and then we can solve for the resonant frequency by using this wave equation, where I have v instead of C because we are not dealing with light anymore, we are dealing with sound in this particular picture and the first frequency is gonna be v over lambda where lambda is 4 times L and this would be an L here. So, that’s our first resonant frequency. The third harmonic is going to be 3 v over 4 L because in this case we have a node here and anti-node here and the next wavelength that fits in this tube such that there is an anti-node in the opening and node at the closed end is… has a… the length of the tube is gonna be 3 quarters of the wavelength in which case lambda is 4 L over 3 and so that’s why we get this equation for the third harmonic frequency and in general, the resonant frequencies for a tube closed at one end then is this integer n times the wave speed over 4 L where n is some odd integer, 1, 3, 5 or so on. So, resonance for this electromagnetic wave from the antenna having a resonant wavelength of the height over 4 is analogous to sound resonance in a closed end tube which has a resonance wavelength of the same form, a length divided by 4. So, the length in this case is length of the tube and the length for the antenna is the height of the antenna. So, the height is analogous to length and further resonance for the antenna might occur at, umm... at some frequencies where n is multiplied by the wave speed which in the case of antenna is C since it's emitting light divided by 4 times the height of the antenna h.
