Question
A 2.50-m-diameter university communications satellite dish receives TV signals that have a maximum electric field strength (for one channel) of . (See Figure 24.28.) (a) What is the intensity of this wave? (b) What is the power received by the antenna? (c) If the orbiting satellite broadcasts uniformly over an area of (a large fraction of North America), how much power does it radiate?
Final Answer
Solution video
OpenStax College Physics, Chapter 24, Problem 35 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
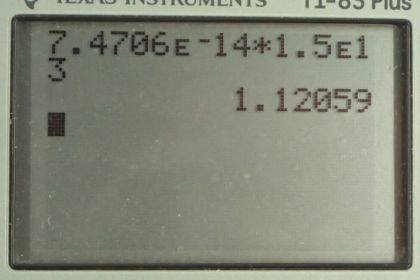
This is College Physics Answers with Shaun Dychko. We are given the electric field strength of the electromagnetic radiations received by the satellite dish and from that we can calculate the intensity of this radiations and its going to be speed of light times the permittivity of free space times electric field strength squared over two. So, that’s three times ten to the eight meters per second times 8.854 times ten to the minus 12 coulomb squared per newton meters squared times 7.5 times ten to the minus six newtons per coulomb squared over two which gives an intensity of the electromagnetic radiations as 7.47 times ten to the minus 14 watts per square meters. The power received by the satellite dish will be this intensity multiplied by its area and we are given its diameter. Now, the area formula for this circular cross-section of the satellite dish is pi times radius squared and then we will substitute diameter divided by two in place of radius. So, this works out to intensity times pi times diameter squared over four and that’s intensity from part A times pi times two and a half meters diameter of the satellite dish squared over four which gives a power received of 3.67 times ten to the minus 13 watts. Now, there is a satellite in orbit around the earth which is broadcasting this signal and we have calculated its intensity in part A and if it is broadcasting that signal in area of North America, what total power output does the satellite have? So that will be the intensity times the area of North America. So, that’s intensity from part A times area of North America which is estimated to be 1.5 times ten to the 13 square meters which gives a total power output of 1.12 watt.