Question
An AM radio transmitter broadcasts 50.0 kW of power uniformly in all directions. (a) Assuming all of the radio waves that strike the ground are completely absorbed, and that there is no absorption by the atmosphere or other objects, what is the intensity 30.0 km away? (Hint: Half the power will be spread over the area of a hemisphere.) (b) What is the maximum electric field strength at this distance?
Final Answer
Solution video
OpenStax College Physics, Chapter 24, Problem 33 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
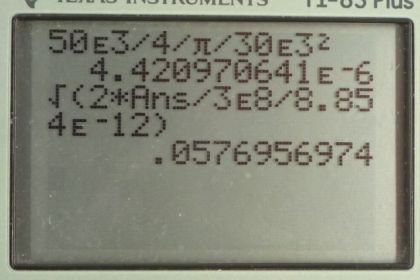
This is College Physics Answers with Shaun Dychko. This AM transmitter is broadcasting with a power of 50 kilo-watts we are told, and we want to know what the intensity is 30 kilo-metres away. Now, gives a bunch of details about the ground completely absorbing the radiations and the atmosphere not absorbing it and all of this is to say that when you get to this point, 30 kilometres away, the only radiation that arrives at this point was directly emitted by the antenna so nothing was reflected off the ground to the spot and nothing was reflected off the air to the spot, its all coming directly from the antenna. So, this means for calculating the intensity we can assume that the power emitted by the antenna is evenly distributed over concentric spheres as you get away from the antenna. So, this point here, we are going to take the power to find this intensity here, we are going to take power divided by the area of the sphere at a distance r from the antenna. So, the area of a sphere is four pi times the radius of the sphere squared and so the intensity then is power divided by four pi r squared so that’s 50 kilo-watts divided by four pi times 30 kilometres and then we square that distance and we get 4.42 times ten to the minus six watts per square meter and the next question that asks us for the peak electric field strength. So, we have the formula telling us that the intensity of the EM wave equals the speed of light times the permittivity of free space times the electric field strength squared over two. So we will solve for E naught by multiplying both sides by two over c epsilon naught and then we square root both sides as well and then we get the electric field strength is the square root of two times the intensity divided by speed of light times permittivity of free space. So, that’s square root of two times 4.42097 times ten to the minus six watts per square meter that we calculated in per day divided by three times ten to the eight meters per second times 8.854 times ten to the minus 12 coulomb square per newton meter squared and this works out to 5.77 times ten to the minus two newtons per coulomb as the electric field strength of this EM wave.