Find the frequency range of visible light, given that it encompasses wavelengths from 380 to 760 nm.

Video Transcript

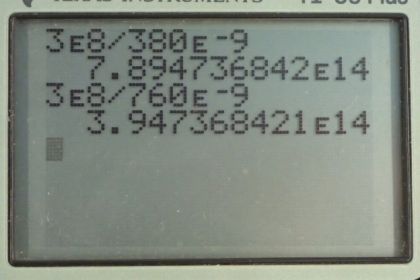
This is College Physics Answers with Shaun Dychko. We're going to determine the possible range of frequencies for visible light. Now, the wave equation says that the speed of light equals its frequency times its wavelength and we can divide both sides by lambda to solve for f. So the frequency is speed of light divided by the wavelength. The maximum possible frequency will be the speed of light divided by the minimum possible wavelength. So that's 3 times 10 to the 8 meters per second, divided by 380 nanometers, which is times 10 to the minus 9 meters. That gives 7.89 times 10 to the 14 Hertz. And then for the minimum frequency, we divide speed of light by the maximum possible wavelength in the visible spectrum. So that's 3 times 10 the 8 meters per second divided by the wavelength of color red, which is 760 times 10 to the minus 9 meters. And this gives 3.95 times 10 to the 14 Hertz. And so the frequency for visible light is between these two numbers.