Question
The laser system tested for inertial confinement can produce
a 100-kJ pulse only 1.00 ns in duration. (a) What is the power output of the laser system during the brief pulse? (b) How many photons are in the pulse, given their wavelength is 1.06 μm? (c) What is the total momentum of all these photons? (d) How does the total photon momentum compare with that of a single 1.00 MeV deuterium nucleus?
Final Answer
- The total photon momentum is greater than the momentum of a deuterium nucleus by a factor of .
Solution video
OpenStax College Physics, Chapter 32, Problem 39 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
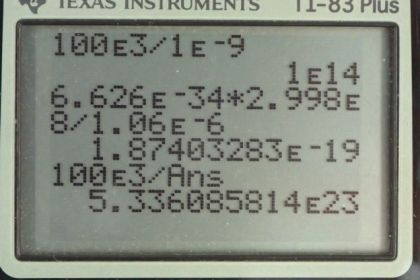
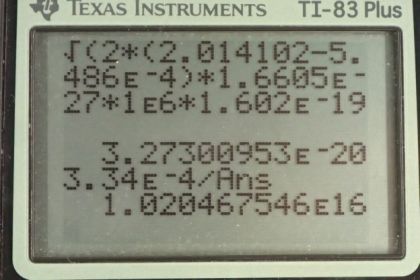
This is College Physics Answers with Shaun Dychko. An inertial confinement laser has an energy output of 100 kilojoules and it lasts for a duration of 1 nanosecond. So what is the power output? So we take that total energy written as 100 times 10 to the 3 joules and divide it by the time of 1 times 10 to the minus 9 seconds and we get 1.00 times 10 to the 14 watts. Part (b) asks us to find how many photons are in this pulse? Well we need to figure out what the energy is per photon and then multiply that by the energy per pulse and then we'll get the number of photons per pulse. So equation 12 in chapter 29 tells us the Planck's constant times the speed of light divided by the wavelength of the photon is the photon energy. So we have Planck's constant times the speed of light divided by the wavelength which we are told is 1.06 micrometers; this works out to 1.874033 times 10 to the minus 19 joules per photon. And then the number of photons then is 100 kilojoules per pulse times 1 photon for every this much many joules and this works out to 5.34 times 10 to the 23 photons in every pulse. Part (c) asks us to find the total momentum of all these photons. Well from equation 30 in chapter 29, we know that the energy of a photon is its momentum times the speed of light so we can divide both sides by c to solve for momentum and this is the momentum of a single photon and the total momentum will be the momentum of a single photon multiplied by the number of photons. So we substitute energy in a photon divided by speed of light in place of momentum multiplied by the number of photons that we calculated in part (b). And so we have this energy per photon that we calculated up here that's written here divided by the speed of light times the number of photons that we calculated here in part (b) written with a few more decimal places. And we get 3.34 times 10 to the minus 4 kilogram meters per second of momentum. And then we are asked in part (e) to compare this momentum of the photons with that of a deuterium nucleus that has a kinetic energy of 1 megaelectron volt. Now we'll assume that that is a non-relativistic amount of energy and so in that case, the kinetic energy of this deuterium nucleus is one-half times the deuterium mass times its speed squared. And we need to know its speed in order to substitute into our non-relativistic momentum formula. So if we multiply both sides by 2 over mass and then take the square root of both sides we end up with this equation for the speed of the deuterium nucleus which we then substitute in for speed in this momentum formula here in red. Now having mass of deuterium multiplied by square root 1 over mass of deuterium, we can move this mass of deuterium into the square root sign; if you prefer, I could write this as square root mass of deuterium squared times 2 times kinetic energy of deuterium and it becomes more clear that this is canceling with one of those and we are left with this here. So we have the square root of 2 times the mass of deuterium nucleus times its kinetic energy is going to be its momentum. So we look up the atomic mass for deuterium in appendix A but we have to keep in mind that these are atomic masses in the word that atomic is important because it means that the electron masses are included in those numbers and so we have to subtract away the mass of an electron from it in order to get the mass of the deuterium nucleus which is what's in brackets here. So we multiply that by 2 times by this conversion factor to turn it into kilograms and multiply it by the kinetic energy which is 1 times 10 to the 6 electron volts converted into joules and then take the square root of all that and we get 3.27 times 10 to the minus 20 kilogram meters per second momentum for a deuterium nucleus that has 1 megaelectron volt of energy. Then we compare the momentum of all the photons in a pulse divided by the momentum of this single deuterium nucleus. So we have 3.34 times 10 to the minus 4 kilogram meters per second — that was our answer for part (d) — divided by the momentum we have just found for the deuterium nucleus and the total photon momentum is greater than the momentum of the deuterium nucleus by a factor of 1.02 times 10 to the 16.
Comments
Wouldn't the factor be 1.02*10^6? I think I might be doing that wrong.
Hi altonbell, as far as I can tell the calculation is correct. To disagree with the answer to part (d) might also require disagreeing with part (c). Did you get the same answer for part (c)? Have you tried typing values into your calculator the same way as in the screenshots? It's hard to tell why you're getting a different answer. My guess, since you're getting the same coefficient (1.02), is that there's a difference in one of your exponents, since your answer differs by a factor of .
All the best,
Shaun