Question
(a) Find the total energy released in MeV in each carbon cycle (elaborated below) including the annihilation energy.
(b) How does this compare with the proton-proton cycle output?
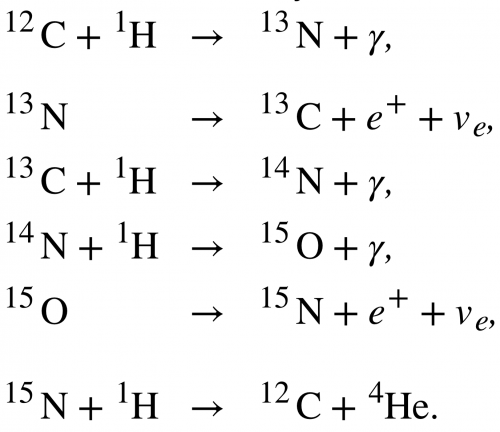
Final Answer
(a)
(b) The energy output is the same as that of the proton-proton cycle.
Solution video
OpenStax College Physics, Chapter 32, Problem 37 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
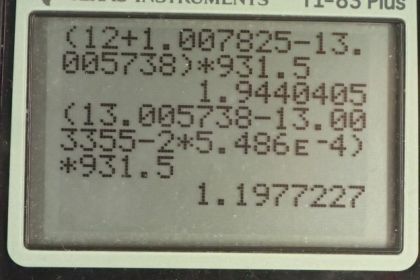
This is College Physics Answers with Shaun Dychko. The carbon cycle of fusion has six different steps and we are going to find the energy released in each of these steps. So in step one, energy subscript 1, we have the difference between the mass of carbon-12 and hydrogen and the mass of nitrogen-13 on the product side. So we find the atomic masses of each of these elements in the appendix A and so it's 12.0 for carbon-12 and then 1.007825 atomic mass units for hydrogen and then minus this amount for nitrogen-13 and there are twelve electrons in carbon-12 and one electron in hydrogen and those masses are included in the atomic masses and there are also a total of thirteen electrons in the nitrogen atom and so these electrons are not something we have to worry about because there are thirteen added here and then thirteen taken away in this atomic mass and so we don't need to account for any difference in number of electrons between the reactants and the products. So we find this difference in the atomic mass and then multiply by 931.5 megaelectron volts per c squared for every atomic mass unit and then multiply by c squared and we get 1.944 megaelectron volts of energy released in the first step of the carbon cycle. Then in step two, nitrogen-13 turns into carbon-13 and a positron and this positron will have the same mass as an electron; the electron neutrino is essentially massless it has negligible mass. So we have mass of nitrogen-13 minus on the reactants side then on the product side we have carbon-13 and then we have the mass of that one positron but then also we have a difference in the number of electrons included in the atomic masses and when I say atom I mean a nucleus with surrounding electrons and the atomic masses given to us in appendix A include all those electrons and they are only twelve electrons in the carbon whereas there are thirteen electrons included in the nitrogen atomic mass and so we have to subtract an additional electron mass in order to take away all of the thirteen electron masses included in the atomic mass for nitrogen. So that explains why there's a factor 2 here because there's one electron mass to account for the different number of electrons between nitrogen and carbon and then there's an additional electron mass to account for this positron. Alright. So that's atomic mass of nitrogen minus atomic mass of carbon-13 minus 2 times the atomic mass of an electron and this works out to 1.198 megaelectron volts. In step three, we have carbon-13 plus hydrogen on the reactant side and then we have nitrogen-14 on the product side a gamma ray has no mass. And so we look up the atomic mass of carbon-13 minus the atomic mass of hydrogen and then take that total sum and minus the atomic mass of nitrogen-14 and then multiply by this conversion factor and we end up with 7.551 megaelectron volts. Then step four, we have nitrogen-14 plus hydrogen on the reactant side take that total atomic mass and then subtract from that oxygen-15. So that's step four and that's what we do here and this works out to 7.297 megaelectron volts. And then in step five, we have oxygen-15 turning into nitrogen-15 plus a positron and so in step five, we have oxygen-15 minus the mass of nitrogen-15 minus 2 times an electron mass and again this factor 2 results from the fact that an oxygen atom has one more electron than a nitrogen atom and so we need to subtract one electron mass to account for that and then additionally there's an electron mass due to the positron on the product side here. So this works out to 1.732 megaelectron volts and then for the last step, we have nitrogen-15 and hydrogen on the reactant side and then carbon-12 and helium-4 on the product side. And so we take the total mass of the reactant side and then subtract mass of the product side and we have the same number of electrons in total on both sides and so we don't need to do any electron mass subtracting or adding or anything; this works out to 4.965 megaelectron volts. Now the overall reaction here is this for the carbon cycle and compare that with the overall proton-proton cycle and it's nearly the same so we have two electrons consumed and four protons and likewise for the carbon cycle. And on the product side, we have helium-4, two electron-neutrino's and six gamma rays helium-4, two electron-neutrino's and seven gamma rays so the only difference is, this six turned into a seven when you'd go from the proton-proton cycle to the carbon cycle. So we expect to get an answer for the overall energy to be released to be very similar to the proton-proton cycle. So we add up each of these numbers that we found in each of these steps here above and we end up with 26.73 megaelectron volts and this factor 4 multiplied by the energy per electron is because we assume that the positron's that are created in steps two and steps five, each of these reacts with an electron because these reactions are taking place in our matter world and so there are always going to be electrons around that will annihilate with these positrons and so they are producing four of the gamma rays that we are including in our overall equation. So there's three gamma rays that are shown here but we have a factor seven written here because four of these gamma rays came from the annihilation of two positrons with two electrons that's also why this equation is written such that we are consuming two electrons; these two electrons are going to be consumed because they will annihilate with two of the positrons so that's a total of four electron masses of energy and that goes into these four of these gamma rays and that's what this term is about here. So we have total of 26.73 megaelectron volts. Now if we compare that with the energy released in the proton-proton cycle, we see that they are essentially the same.