Question
If everyone in Australia received an extra 0.05 mSv per year of radiation, what would be the increase in the number of cancer deaths per year? (Assume that time had elapsed for the effects to become apparent.) Assume that there are deaths per Sv of radiation per year. What percent of the actual number of cancer deaths recorded is
this?
Final Answer
25 additional deaths per year.
This represents an increase of 0.05% above the actual number of cancer deaths per year in Australia.
Solution video
OpenStax College Physics, Chapter 32, Problem 25 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
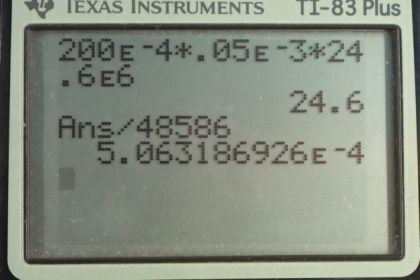
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. If everyone in Australia received an extra 0.05 millisieverts of radiation exposure per year, how many additional deaths would you expect to see each year? So we assume that there are 200 times 10 to the minus 4 deaths per sievert per year and then we multiply this by the additional exposure—0.05 millisieverts— and then times by the number of people which is 24.6 times 10 to the 6 people— that's something I found using Google— and that would be about 25 additional deaths per year expected. And looking at the number of total cancer deaths in Australia every year using the website canceraustralia.gov.au, there are 48586 people dying per year of cancer in Australia and so this 24.6 additional deaths per year as a result of the additional 0.05 millisievert exposure every year is only 0.05 percent of what happens otherwise.