Question
It is estimated that weapons tests in the atmosphere have deposited approximately 9 MCi of on the surface of the
earth. Find the mass of this amount of .
Final Answer
Solution video
OpenStax College Physics, Chapter 32, Problem 59 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
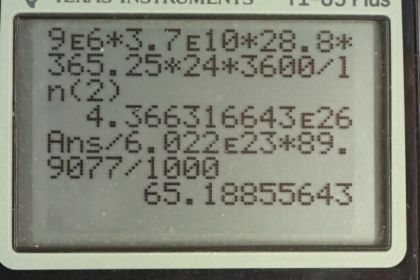
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In the battle days when nuclear weapons tests took place above ground and the atmosphere, about 9 megacuries worth of strontium-90 were put into the atmosphere and so the question is what mass of strontium-90 is that? Well, activity based on equation 48 from chapter 31 is natural logarithm of 2 multiplied by the number of atoms divided by the half-life of the material. So we'll find the number of atoms and then we'll use that to figure out the mass after we look up the molar mass in appendix A. So we rearrange this by multiplying both sides by t 1/2 divided by ln of 2 and we end up with number of atoms of strontium-90 is the activity times the half-life divided by natural logarithm of 2. So that's 9 megacuries and converted into becquerels because becquerels is the mks unit. So we'll multiply by 3.70 times 10 to the 10 becquerels for every curie and then multiply by the half-life of strontium-90 and we look this up in appendix A. So that's 28.8 years converted into seconds and divide by natural logarithm of 2 and we get 4.36632 times 10 to the 26 atoms of strontium-90. Then we have to convert that number of atoms into a mass. So we multiply by 1 mole for every 6.022 times 10 to the 23 atoms— this is dividing by Avogadro's number— and then we multiply by the molar mass that we look up in appendix A so that's 89.9077 grams for every mol and the mols cancel, atoms cancel and then we convert that into kilograms and we end up with 70 kilograms of strontium-90 in the atmosphere due to nuclear weapons tests.