Question
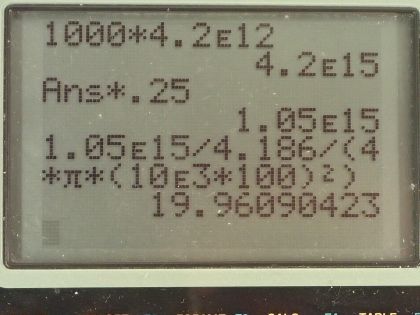
A 1.00-MT bomb exploded a few kilometers above the
ground deposits 25.0% of its energy into radiant heat.
(a) Find the calories per at a distance of 10.0 km by assuming a uniform distribution over a spherical surface of
that radius.
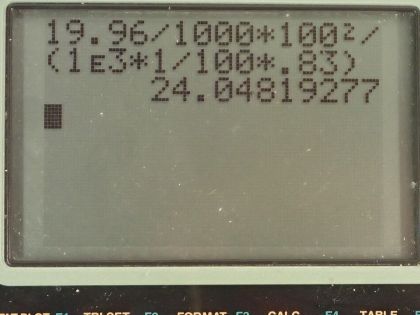
(b) If this heat falls on a person's body, what temperature increase does it cause in the affected tissue, assuming it is absorbed in a layer 1.00-cm deep?
Final Answer
Note At 1:03 Shaun mis-spoke in saying is the area of a circle. It's the surface area of a sphere. The energy is distributed uniformly over the surface of a sphere, not a circle.
Solution video
OpenStax College Physics, Chapter 32, Problem 60 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Suppose a 1.00 megaton bomb explodes a few kilometers above the ground, we convert this energy into joules by multiplying by 4.2 times 10 to the 12 joules for every kiloton and we convert the megatons into kilotons by multiplying by a 1000 there and that's 4.2 times 10 to the 15 joules. 25 percent of this energy is turned into radiant heat and so we multiply that by 0.25 to get 1.05 times 10 to the 15 joules of heat energy and a distance of 10.0 kilometers away is 10.0 times 10 to the 3 meters and the question is what will be the calories per square centimeter at this distance of 10.0 kilometers away from the explosion? So this is a type of flux so I have this symbol here equals the energy divided by the amount of area over which that energy is spread. So the area is the area of a circle with this radius of 10.0 kilometers and that is 4πr squared is the surface area of a circle so we substitute that in place of area here. So that's 1.05 times 10 to the 15 joules multiplied by 1 calorie for every 4.186 joules because the question asks us to give our answer in calories per square centimeter and we divide that by 4π times this radius, which we also convert into centimeters and to square that and we get 20.0 calories per square centimeter. In part (b), we are asked] supposing that the energy is absorbed into a depth of 1.00 centimeter of skin tissue by how much will it increase the temperature of that skin? So we need to look up the specific heat of skin and we look at table [14.1] and the human body has a specific heat of about 0.83 kilocalories per kilogram per Celsius degree and we also need to know the density of the human body, which we look up in table [11.1] and we will assume it's the same as that of water which is 1.000 times 10 to the 3 kilograms per cubic meter and yeah, the depth is 1.00 centimeters so we have written down all the stuff that we need to know here. So here's a formula from chapter 14, which says the heat absorbed equals the mass times the specific heat of the substance times its change in temperature and ultimately we want to find what is this ΔT? Now we don't know the energy absorbed but we do know the energy per area. So if we divide this left side by area we can also divide the right-hand side by area and the equation is still true, we are just dividing both sides by the same thing and so let's find an expression then for mass per area because this Q per area, this energy per area is the answer to part (a) this is Q per A— that's the left side— so now the task is then to figure out what is this mass per area of the human body? So the density is mass divided by volume and volume is the depth multiplied by the area for a rectangle so if you have a rectangle here with an area of A on the top and it has some depth here— we'll call this d— then the volume of this is the area multiplied by the depth d so we substitute dA in place of V. Now we can solve this for m over A then by multiplying both sides by d so m over A then is density times the depth. So we substitute this in place of m over A and we do that here and now we'll solve for ΔT so we divide both sides by density times depth times specific heat. And so the change in temperature then is the energy absorbed per area divided by the density times the depth through over which it's absorbed times specific heat. So that's 19.96 calories per square centimeter and we are going to convert this into kilocalories per square meter. We need to have square meters in order to match with this density, which has units of kilograms per cubic meter; this depth also has to be converted into meters for the same reason and we want kilocalories here because our specific heat has units of kilocalories. So we have 19.96 calories per square meter times 1.00 kilocalorie for every 1000 calories times 100 centimeters for every meter and we do that twice and we have meters squared on the top then or per meters squared I should say and then divide that by 1.00 times 10 to the 3 kilograms per cubic meter times 1.00 centimeter converted into meters times 0.83 kilocalories per kilogram per Celsius degree and we get a temperature change then of 24 Celsius degrees.
Comments
The area of a circle is not 4*pi*r^2. it is simply pi*r^2. I believe you are thinking of the area of a circle with it's diameter and confusing the denominator. That is 1/4*pi*d^2
Hi Alton, thank you very much for noticing this issue. The formula is correct, but I mis-spoke in saying it's the area of a circle. is the surface area of a sphere. The energy is distributed uniformly over the surface of a sphere. The working is correct, but I should have said sphere instead of circle. I have added a note in the final answer section.
All the best,
Shaun