Question
The electrical power output of a large nuclear reactor facility is 900 MW. It has a 35.0% efficiency in converting nuclear power to electrical.
(a) What is the thermal nuclear power output in megawatts?
(b) How many nuclei fission each second, assuming the average fission produces 200 MeV?
(c) What mass of is fissioned in one year of full-power operation?
Final Answer
Solution video
OpenStax College Physics, Chapter 32, Problem 49 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
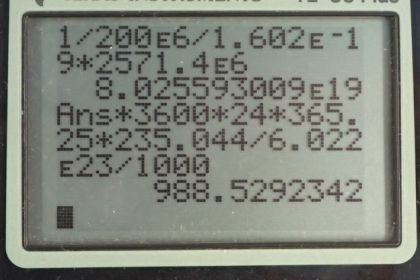
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A nuclear power plant has an electrical power output of 900 megawatts and an efficiency of 35 percent. And so the question is what is the total thermal output of the nuclear reactions only 35 percent of which is going into this 900 megawatts of electrical power? So the electrical output is 0.350 times the total and so the total we can find by dividing both sides by 0.350. So we have the electrical power output divided by 0.350 which is 900 megawatts divided by 0.350 which is 2570 megawatts being produced. So this is a total thermal rate of energy the rate of thermal energy production. OK So in part (b) we are asked what number of uranium-235 nuclei fission? And so we are told that one fission produces 200 megaelectron volts so we'll write that as 200 times 10 to the 6 electron volts and then convert this into joules so we have 1 electron volt for every 1.602 times 10 to the minus 19 joules. And so we have one fission for every you know, this many joules after you do this calculation and then multiply that by the number of joules per second total thermal power. So that's multiplying by 2571.4 times 10 to the 6 joules per second and then these joules cancel and we are left with fissions per second. So that's 8.03 times 10 to the 19 uranium-235 nuclei fission every second which is a mind bogglingly large number. OK And then what total mass of uranium-235 will fission in a year? So based on this number of fissions per second that we calculated in part (b), we'll times that by you'll find the number of fissions per year after we multiply by each of these factors times by 3600 seconds per hour and then 24 hours per day and then 365.25 days per year. So that's the number of fissions per year and then multiply that by 1 mol for every 6.022 times 10 to the 23 nuclei so we are basically dividing by Avogadro's number here. So this number of nuclei fissioning cancels so we are left with mols per year and then we times by 235.044 grams per mol so that's the number of grams per year and then multiply by 1 kilogram for every 1000 grams. So we have 989 kilograms per year of uranium-235 fissioning.